Question

16．已知集合A={x|1≤x≤6}，关于x的二次方程：$\frac{1}{4}$x²+$\sqrt{b}$x+2c=0．
请回答下列问题：
（Ⅰ）若b，c∈A，且c，c∈Z，求该二次方程有解的概率；
（Ⅱ）若b，c∈A，求该二次方程有解的概率．

Answer 1

分析 （I）根据判别式△≥0得出一元二次方程有实根的条件b≥2c，由b，c∈{1，2，3，4，5，6}，列出基本事件数，计算对应的概率即可；
（II）利用几何概型求出对应的概率即可．

解答 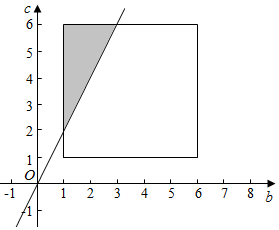解：（Ⅰ）要使得关于x的二次方程：$\frac{1}{4}$x²+$\sqrt{b}$x+2c=0有解，
只要△≥0，即要b-2c≥0，
即b≥2c，
又∵b，c∈A，且c，c∈Z，
∴b，c∈{1，2，3，4，5，6}，
∴（b，c）的所有可能的取值情况种数为25种，
∴满足条件的（b，c）的所有可能的取值情况为：（2，1），（3，1），（4，1），（4，2），（5，1），（5，2），（6，1），（6.2），（6，3）
∴该二次方程有解的概率为$\frac{9}{25}$；
（Ⅱ）由（Ⅰ）知，本概率模型下的总测度为：
平面区域$\left\{\begin{array}{l}{1≤b≤6}\\{1≤c≤6}\end{array}\right.$所围成的正方形的面积，
使得该二次方程有解的不等式为b≥2c，
则本概率模型的有效测度为直线b=2c与此正方形所围成的
三角形的面积（如图中阴影部分），
易知：正方形的面积为25，三角形的面积为4，
∴P=$\frac{4}{25}$为所求的概率．

点评 本题考查了用列举法求古典概型的概率问题，也考查了几何概型的应用问题，是中档题．