
【题目】在△ABC中,a=x,b=2,B=45°,若此三角形有两解,则x的取值范围是( )
A.x>2
B.x<2
C.![]()
D.![]()
【答案】C
【解析】解: ![]() =2
=2 ![]() ∴a=2
∴a=2 ![]() sinA
sinA
A+C=180°﹣45°=135°
A有两个值,则这两个值互补
若A≤45°,则C≥90°,
这样A+B>180°,不成立
∴45°<A<135°
又若A=90,这样补角也是90°,一解
所以 ![]() <sinA<1
<sinA<1
a=2 ![]() sinA
sinA
所以2<a<2 ![]()
故选C
利用正弦定理和b和sinB求得a和sinA的关系,利用B求得A+C;要使三角形两个这两个值互补先看若A≤45°,则和A互补的角大于135°进而推断出A+B>180°与三角形内角和矛盾;进而可推断出45°<A<135°若A=90,这样补角也是90°,一解不符合题意进而可推断出sinA的范围,利用sinA和a的关系求得a的范围.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,
, ![]() 是坐标原点,
是坐标原点, ![]() 分别为其左右焦点,
分别为其左右焦点, ![]() ,
, ![]() 是椭圆上一点,
是椭圆上一点, ![]() 的最大值为
的最大值为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]()
(i)求证: ![]() 为定值;
为定值;
(ii)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() 相切,且与
相切,且与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() .若动点
.若动点![]() 与两定点
与两定点![]() 所构成三角形的周长为6.
所构成三角形的周长为6.
(Ⅰ) 求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ) 设斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,当
两点,当![]() ,且
,且![]() 位于直线
位于直线![]() 的两侧时,证明:
的两侧时,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x﹣cosx,{an}是公差为 ![]() 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
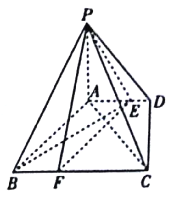
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=1,an+an+1=( ![]() )n , Sn=a1+4a2+42a3+…+4n﹣1an , 类比课本中推导等比数列前项和公式的方法,可求得5Sn﹣4nan= .
)n , Sn=a1+4a2+42a3+…+4n﹣1an , 类比课本中推导等比数列前项和公式的方法,可求得5Sn﹣4nan= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com