
【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明:![]() 为等比数列;
为等比数列;
(3)求数列{an}的通项公式.
【答案】见解析
【解析】(1)解:当n=2时,4S4+5S2=8S3+S1,
即4(a1+a2+a3+a4)+5(a1+a2)=8(a1+a2+a3)+a1,
整理得a4=![]() ,
,
又a2=![]() ,a3=
,a3=![]() ,
,
所以a4=![]() .
.
(2)证明:当n≥2时,有4Sn+2+5Sn=8Sn+1+Sn-1,
即4Sn+2+4Sn+Sn=4Sn+1+4Sn+1+Sn-1,
∴4(Sn+2-Sn+1)=4(Sn+1-Sn)-(Sn-Sn-1),
即an+2=an+1-![]() an(n≥2).
an(n≥2).
经检验,当n=1时,上式成立.
∵ =
= =
= =
=![]() 为常数,且a2-
为常数,且a2-![]() a1=1,
a1=1,
∴数列![]() 是以1为首项,
是以1为首项,![]() 为公比的等比数列.
为公比的等比数列.
(3)解:由(2)知,an+1-![]() an=
an=![]() (n∈N*),
(n∈N*),
等式两边同乘2n,
得2nan+1-2n-1an=2(n∈N*).
又20a1=1,
∴数列{2n-1an}是以1为首项,2为公差的等差数列.
∴2n-1an=2n-1,
即an=![]() (n∈N*).
(n∈N*).
则数列{an}的通项公式为an=![]() (n∈N*).
(n∈N*).


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:
【题目】某学校进行体验,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50个身高介于155 ![]() 到195
到195![]() 之间),现将抽取结果按如下方式分成八组:第一组
之间),现将抽取结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() ,并按此分组绘制如图所示的频率分布直方图,其中第六组
,并按此分组绘制如图所示的频率分布直方图,其中第六组![]() 和第七组
和第七组![]() 还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.
还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.
(1)补全频率分布直方图;
(2)根据频率分布直方图估计这50位男生身高的中位数;
(3)用分层抽样的方法在身高为![]() 内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在
内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|(x-3)(x+a)<0,a∈R},集合B={x∈Z|x2-3x-4<0}.
(1)若A∩B的子集个数为4,求a的范围;
(2)若a∈Z,当A∩B≠![]() 时,求a的最小值,并求当a取最小值时A∪B.
时,求a的最小值,并求当a取最小值时A∪B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司有一款保险产品的历史收益率(收益率![]() 利润
利润![]() 保费收入)的频率分布直方图如图所示:
保费收入)的频率分布直方图如图所示:
(1)试估计这款保险产品的收益率的平均值;
(2)设每份保单的保费在20元的基础上每增加![]() 元,对应的销量为
元,对应的销量为![]() (万份).从历史销售记录中抽样得到如下5组
(万份).从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表,知![]() 与
与![]() 有较强的线性相关关系,且据此计算出的回归方程为
有较强的线性相关关系,且据此计算出的回归方程为![]() .
.

(ⅰ)求参数![]() 的值;
的值;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入
的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入![]() 每份保单的保费
每份保单的保费![]() 销量.
销量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款 | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() ,
,![]() 得到下表2:
得到下表2:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]()
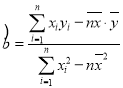
![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com