
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款 | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() ,
,![]() 得到下表2:
得到下表2:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]()
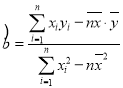
![]() )
)
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格![]() (元)与时间
(元)与时间![]() (天)组成有序数对
(天)组成有序数对![]() ,点
,点![]() 落在图中的两条线段上.
落在图中的两条线段上.
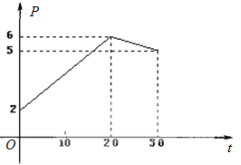
该股票在30天内的日交易量![]() (万股)与时间
(万股)与时间![]() (天)的部分数据如下表所示:
(天)的部分数据如下表所示:
第 | 4 | 10 | 16 | 22 |
| 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该股票每股交易价格![]() (元)与时间
(元)与时间![]() (天)所满足的函数关系式;
(天)所满足的函数关系式;
(2)根据表中数据,写出日交易量![]() (万股)与时间
(万股)与时间![]() (天)的一次函数关系式;
(天)的一次函数关系式;
(3)用![]() (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出![]() 关于
关于![]() 的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明:![]() 为等比数列;
为等比数列;
(3)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1,a14=b4.
(1)求{an}的通项公式;
(2)设cn=an+bn,求数列{cn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过定点P(-2,1)作直线l分别与x、y轴交于A、B两点,
(1)求经过点P且在两坐标轴上的截距相等的直线l方程.
(2)求使![]() 面积为4时的直线l方程。
面积为4时的直线l方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 越大,说明“
越大,说明“![]() 与
与![]() 有关系”的可信度越大.
有关系”的可信度越大.
②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() 的值分别是
的值分别是![]() 和0.3.
和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为![]() 中,
中, ![]() ,
,
则![]() .正确的个数是( )
.正确的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过坐标原点,其到函数为
的图像经过坐标原点,其到函数为![]() ,数列的前
,数列的前![]() 项和为
项和为![]() ,点
,点![]()
![]() 均在函数
均在函数![]() 的图像上.
的图像上.
(I)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() n项和,求使得
n项和,求使得![]() <
<![]() 对所有都成立的最小正整数m.
对所有都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com