
【题目】四棱锥P﹣ABCD中,PA⊥底面ABCD,且PA=AB=AD=![]() CD,AB∥CD,∠ADC=90°.
CD,AB∥CD,∠ADC=90°.
(1)在侧棱PC上是否存在一点Q,使BQ∥平面PAD?证明你的结论;
(2)求证:平面PBC⊥平面PCD;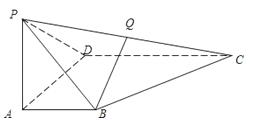
【答案】
解:(1)当Q为侧棱PC中点时,有BQ∥平面PAD.
证明如下:如图,取PD的中点E,连AE、EQ.
∵Q为PC中点,则EQ为△PCD的中位线,
∴EQ∥CD且EQ=![]() CD.
CD.
∵AB∥CD且AB=![]() CD,∴EQ∥AB且EQ=AB,
CD,∴EQ∥AB且EQ=AB,
∴四边形ABQE为平行四边形,则BQ∥AE.
∵BQ平面PAD,AE平面PAD,
∴BQ∥平面PAD.
(2)证:∵PA⊥底面ABCD,∴PA⊥CD.
∵AD⊥CD,PA∩AD=A,∴CD⊥平面PAD.
∵AE平面PAD,∴CD⊥AE.
∵PA=AD,E为PD中点,∴AE⊥PD.
∵CD∩PD=D,∴AE⊥平面PCD.
∵BQ∥AE,∴BQ⊥平面PCD.
∵BQ平面PBC,∴平面PBC⊥平面PCD.
【解析】(1)当Q为侧棱PC中点时,有BQ∥平面PAD.取PD的中点E,连AE、EQ.只需证明平面PAD外的直线BQ平行于平面PAD内的直线AE,即可.
(2)要证平面PBC⊥平面PCD,只需证明AE垂直平面PAD内的两条相交直线CD、PD,BQ∥AE,BQ平面PBC即可;
【考点精析】掌握直线与平面平行的性质和平面与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行;一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1=﹣an2+2an , n∈N* , 且a1=0.9,令bn=lg(1﹣an);
(1)求证:数列{bn}是等比数列;
(2)求数列{ ![]() }各项和.
}各项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【苏北四市2016-2017学年度高三年级第一学期期末调研】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且右焦点
,且右焦点![]() 到左准线的距离为
到左准线的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为椭圆
为椭圆![]() 的左顶点,
的左顶点,![]() 为椭圆
为椭圆![]() 上位于
上位于![]() 轴上方的点,直线
轴上方的点,直线![]() 交
交![]() 轴于点
轴于点
![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() .
.
(ⅰ)当直线的![]() 斜率为
斜率为![]() 时,求
时,求![]() 的外接圆的方程;
的外接圆的方程;
(ⅱ)设直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设an= ![]() sin
sin ![]() ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
A.25
B.50
C.75
D.100
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人从一鱼池中捕得120条鱼,做了记号之后,再放回池中,经过适当的时间后,再从池中捕得100条鱼,结果发现有记号的鱼为10条(假定鱼池中不死鱼,也不增加),则鱼池中大约有鱼( )
A.120条
B.1200条
C.130条
D.1000条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次模拟考试后,从高三某班随机抽取了20位学生的数学成绩,其分布如下:
分组 | [90,100] | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
频数 | 1 | 2 | 6 | 7 | 3 | 1 |
分数在130分(包括130分)以上者为优秀,据此估计该班的优秀率约为( )
A.10%
B.20%
C.30%
D.40%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张老师给学生出了一道题,“试写一个程序框图,计算S=1+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() ”.发现同学们有如下几种做法,其中有一个是错误的,这个错误的做法是( )
”.发现同学们有如下几种做法,其中有一个是错误的,这个错误的做法是( )
A.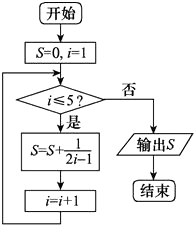
B.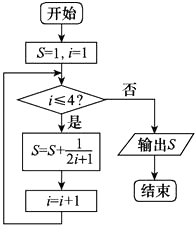
C.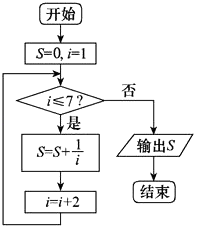
D.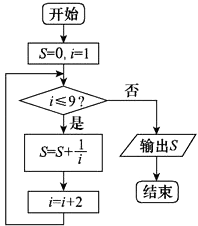
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正数数列{an}的前n项和为Sn , 点P(an , Sn)在函数f(x)= ![]() x2+
x2+ ![]() x上,已知b1=1,3bn﹣2bn﹣1=0(n≥2,n∈N*),
x上,已知b1=1,3bn﹣2bn﹣1=0(n≥2,n∈N*),
(1)求数列{an}的通项公式;
(2)若cn=anbn , 求数列{cn}的前n项和Tn;
(3)是否存在整数m,M,使得m<Tn<M对任意正整数n恒成立,且M﹣m=9,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com