
(本小题满分12分)已知向量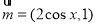 ,
,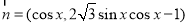 ,函数
,函数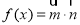 .
.
(1)求函数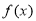 的单调递增区间;
的单调递增区间;
(2)在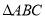 中,角
中,角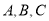 的对边分别为
的对边分别为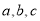 ,若
,若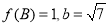 ,
, ,求
,求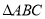
的面积.
科目:高中数学 来源:2014-2015学年豫晋冀高三上学期第二次调研考试文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,输出S的值为( )
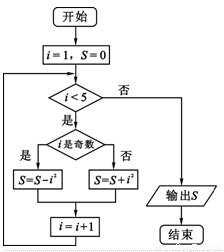
A.3 B.-6 C.10 D.12
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省宜宾市高三第一次诊断考试文科数学试卷(解析版) 题型:选择题
函数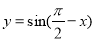 的图象 ( )
的图象 ( )
(A)关于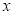 轴对称 (B)关于
轴对称 (B)关于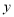 轴对称
轴对称
(C)关于原点对称 (D)关于直线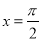 对称
对称
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省宜宾市高三第一次诊断考试理科数学试卷(解析版) 题型:选择题
有七名同学站成一排照毕业纪念照,其中小明必须站在正中间,并且小李、小张两位同学要站在一起,则不同的站法有( )
(A)192种 (B)120种 (C)96种 (D)48种
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省高三一诊模拟文科数学试卷(解析版) 题型:解答题
(本小题满分14分)设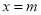 和
和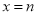 是函数
是函数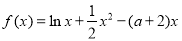 的两个极值点,其中
的两个极值点,其中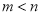 ,
,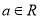 .
.
(1)若曲线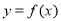 在点
在点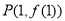 处的切线垂直于
处的切线垂直于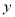 轴,求实数
轴,求实数 的值;
的值;
(2)求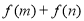 的取值范围;
的取值范围;
(3)若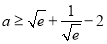 ,求
,求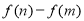 的最大值(
的最大值(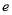 是自然对数的底数).
是自然对数的底数).
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省高三一诊模拟文科数学试卷(解析版) 题型:选择题
已知直线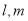 和平面
和平面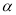 ,则下列命题正确的是( )
,则下列命题正确的是( )
A.若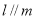 ,
, ,则
,则
B.若 ,
,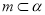 ,则
,则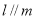
C.若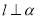 ,
,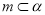 ,则
,则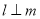
D.若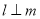 ,
,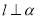 ,则
,则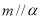
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省高三一诊模拟理科数学试卷(解析版) 题型:选择题
下列命题:①若直线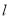 上有无数个点不在平面
上有无数个点不在平面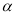 内,则
内,则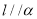 ;
;
②若直线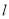 与平面
与平面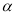 平行,则
平行,则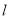 与平面
与平面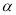 内的任意一条直线都平行;
内的任意一条直线都平行;
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行;
④若直线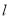 与平面
与平面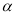 平行,则
平行,则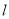 与平面
与平面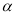 内的任意一条直线都没有公共点.
内的任意一条直线都没有公共点.
其中正确的个数是( )
A. B.
B.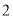 C.
C.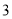 D.
D.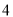
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省连云港、徐州、淮安、宿迁四市高三一模考试文科数学试卷(解析版) 题型:解答题
(本小题满分16分)在数列 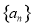 中,已知
中,已知 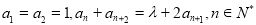 ,
,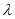 为常数.
为常数.
(1)证明: 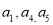 成等差数列;
成等差数列;
(2)设 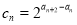 ,求数列 的前n项和
,求数列 的前n项和 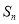 ;
;
(3)当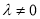 时,数列
时,数列 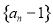 中是否存在三项
中是否存在三项 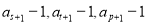 成等比数列,且
成等比数列,且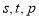 也成等比数列?若存在,求出
也成等比数列?若存在,求出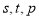 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com