
 如图,△ABC的外接圆⊙O的半径为
如图,△ABC的外接圆⊙O的半径为| 5 |
| ||
| 21 |
| 2 |
| 7 |
| ||
| 21 |
| 2 |
| 7 |
| 2 |
| 7 |
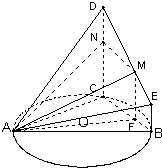 解:(1)∵CD⊥平面ABC,BE∥CD
解:(1)∵CD⊥平面ABC,BE∥CD| BE |
| AE |
| ||
| 21 |
| 21 |
| AE2-BE2 |
| 5 |
| 5 |
| AB2-BC2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 20 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| AF2+MF2 |
| AC2+CF2+MF2 |
16+x2+(4-
|
| MN |
| AM |
| x | ||||
|
| 2 |
| 7 |
| 8 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
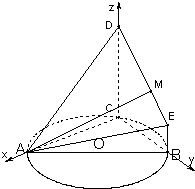 :
:| DE |
| OB |
| DM |
| DM |
| DE |
|
|
| AM |
| AM |
| OB |
| |2λ×2| | ||
2•
|
| 2 |
| 7 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 7 |


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
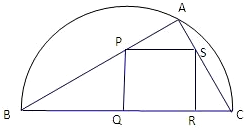 如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=20米,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=20米,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值| S1 | S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
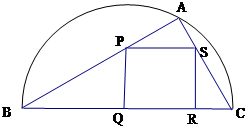 如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值| S1 | S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
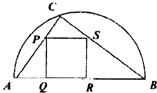 如图,某小区准备绿化一块直径为AB的半圆形空地,点C在半圆弧上,半圆内△ABC外的地方种草,△ABC的内接正方形PQRS内部为一水池,其余地方种花,若AB=2a,∠CAB=θ,设△ABC的面积为S1,正方形PQRS的边长为x,面积为S2,将比值
如图,某小区准备绿化一块直径为AB的半圆形空地,点C在半圆弧上,半圆内△ABC外的地方种草,△ABC的内接正方形PQRS内部为一水池,其余地方种花,若AB=2a,∠CAB=θ,设△ABC的面积为S1,正方形PQRS的边长为x,面积为S2,将比值| S1 |
| S2 |
| 2asin2θ |
| 2+sin2θ |
查看答案和解析>>
科目:高中数学 来源: 题型:
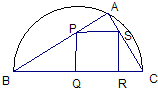 (2007•杨浦区二模)如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
(2007•杨浦区二模)如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值| S1 | S2 |
查看答案和解析>>
科目:高中数学 来源:2007年上海市杨浦区、静安区高考数学二模试卷(文理合卷)(解析版) 题型:解答题
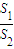 称为“规划合理度”.
称为“规划合理度”.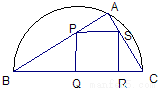
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com