
【题目】设函数![]() ,
,![]() R.
R.
(Ⅰ)求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若对任意的实数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,若对任意的实数
,若对任意的实数![]() ,关于
,关于![]() 的方程
的方程![]() 有且只有两个不同的实根,求实数
有且只有两个不同的实根,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)-1(Ⅲ)
(Ⅱ)-1(Ⅲ)![]() 或
或![]()
【解析】
(Ⅰ)求出函数在![]() 处的导数后可得切线方程.
处的导数后可得切线方程.
(Ⅱ)参变分离后求函数![]() 的最小值可得
的最小值可得![]() 的最大值.
的最大值.
(Ⅲ)因为![]() ,故
,故![]() 无零根,参变分离后考虑
无零根,参变分离后考虑![]() 的图像与直线
的图像与直线![]() 总有两个不同的交点,从而得到实数
总有两个不同的交点,从而得到实数![]() 的取值范围.
的取值范围.
(Ⅰ)![]() ,
,![]() . 且
. 且![]() ,所以在
,所以在![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅱ)因为对任意的实数![]() ,不等式
,不等式![]() 恒成立.所以
恒成立.所以![]() 恒成立.
恒成立.
设![]() ,则
,则![]()
![]()
![]() ,
,
所以![]() 在
在![]() ,
,![]() 单调递增,在
单调递增,在![]() ,
,![]() 单调递减.
单调递减.
所以![]() ,
,
因为![]() ,
,![]() 是方程
是方程![]() 的两根.
的两根.
所以![]()
![]()
![]()
![]()
![]() . (其中
. (其中![]() )
)
所以![]() 的最大值为
的最大值为![]() .
.
(Ⅲ)若对任意的实数![]() ,关于
,关于![]() 的方程
的方程![]() 有且只有两个不同的实根,
有且只有两个不同的实根,
当![]() ,得
,得![]() ,与已知矛盾.
,与已知矛盾.
所以![]() 有两根,即
有两根,即![]() 与
与![]() 有两个交点
有两个交点
令![]() ,则
,则![]() .
.
令![]() ,
,![]() ,则
,则![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,所以
单调递增,所以![]() .
.
(ⅰ)当![]() 时,即
时,即![]() 时,则
时,则![]() ,即
,即![]() 在
在![]() ,
,![]() 单调递增,且当
单调递增,且当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ;当
;当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() .此时对任意的实数
.此时对任意的实数![]() ,原方程恒有且只有两个不同的解.
,原方程恒有且只有两个不同的解.
(ⅱ)当![]() 时,
时,![]() 有两个非负根
有两个非负根![]() ,
,![]() ,所以
,所以![]() 在
在![]() ,
,![]() ,
,![]() 单调递增,
单调递增,![]() 单调递减,所以当
单调递减,所以当![]() 时有4个交点,
时有4个交点,![]() 或
或![]() 有3个交点,均与题意不合,舍去.
有3个交点,均与题意不合,舍去.
(ⅲ)当![]() 时,则
时,则![]() 有两个异号的零点
有两个异号的零点![]() ,
,![]() ,不妨设
,不妨设![]() ,则
,则![]() 在
在![]() ,
,![]() 单调递增;
单调递增;![]() 在
在![]() ,
,![]() 单调递减.
单调递减.
当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,
,
当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,
,
所以当![]() 时,对任意的实数
时,对任意的实数![]() ,原方程恒有且只有两个不同的解.
,原方程恒有且只有两个不同的解.
所以有![]() ,
,![]() ,得
,得![]() .
.
由![]() ,得
,得![]() ,即
,即![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
故![]()
![]()
![]() .所以
.所以![]() .
.
所以当![]() 或
或![]() 时,原方程对任意实数
时,原方程对任意实数![]() 均有且只有两个解.
均有且只有两个解.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面是边长为
的底面是边长为![]() 的菱形,
的菱形,![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,点
,点![]() 在平面
在平面![]() 的射影为
的射影为![]() ,
,![]() 为棱
为棱![]() 上一点,
上一点,
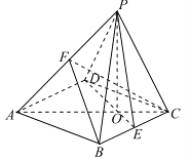
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,侧面![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,E,Q分别是BC和PC的中点.
,E,Q分别是BC和PC的中点.
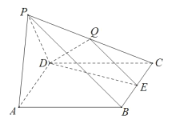
(I)求直线BQ与平面PAB所成角的正弦值;
(Ⅱ)求二面角E-DQ-P的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
![]()
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量![]() (单位:瓶)的分布列;
(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),当六月份这种酸奶一天的进货量
(单位:元),当六月份这种酸奶一天的进货量![]() (单位:瓶)为多少时?
(单位:瓶)为多少时?![]() 的数学期望达到最大值?
的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明口袋中有3张10元,3张20元(因纸币有编号认定每张纸币不同),现从中掏出纸币超过45元的方法有_______种;若小明每次掏出纸币的概率是等可能的,不放回地掏出4张,刚好是50元的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了![]() 位育龄妇女,结果如表.
位育龄妇女,结果如表.
非一线 | 一线 | 总计 | |
愿生 |
|
|
|
不愿生 |
|
|
|
总计 |
|
|
|
附表:
|
|
|
|
|
|
|
|
由![]() 算得,
算得,![]() 参照附表,得到的正确结论是( )
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别有关”
的前提下,认为“生育意愿与城市级别有关”
B. 有![]() 以上的把握认为“生育意愿与城市级别有关”
以上的把握认为“生育意愿与城市级别有关”
C. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别无关”
的前提下,认为“生育意愿与城市级别无关”
D. 有![]() 以上的把握认为“生育意愿与城市级别无关”
以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人进行定点投篮活动,已知他们每投篮一次投中的概率分别是![]() 和
和![]() ,每次投篮相互独立互不影响.
,每次投篮相互独立互不影响.
(Ⅰ)甲乙各投篮一次,记“至少有一人投中”为事件A,求事件A发生的概率;
(Ⅱ)甲乙各投篮一次,记两人投中次数的和为X,求随机变量X的分布列及数学期望;
(Ⅲ)甲投篮5次,投中次数为ξ,求ξ=2的概率和随机变量ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年,国际数学协会正式宣布,将每年的3月14日设为“国际数学节”,其来源是中国古代数学家祖冲之的圆周率,为庆祝该节日,某校举办的“数学嘉年华”活动中,设计了如下的有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,则分别获得5个、10个、20个学豆的奖励.游戏还规定:当选手闯过一关后,可以选择带走相应的学豆,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部学豆归零,游戏结束.设选手甲能闯过第一关、第二关、第三关的概率分别为![]() ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为![]() ,且各关之间闯关成功与否互不影响.
,且各关之间闯关成功与否互不影响.
(1)求选手甲第一关闯关成功且所得学豆为零的概率;
(2)设该选手所得学豆总数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com