Question

17．读程序（如图）

（Ⅰ）画出程序框图；
（Ⅱ）当输出的y的范围大于1时，求输入的x值的取值范围．

Answer 1

分析 （Ⅰ）由已知中的程序语句，可知该程序包含一个条件结构，结合语句给出相应的框图，可得答案．
（Ⅱ）分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算分段函数 y=$\left\{\begin{array}{l}{\sqrt{x}}&{x＞0}\\{（\frac{1}{2}）^{x}-1}&{x≤0}\end{array}\right.$的函数值，由已知分类讨论即可得解．

解答 解：（Ⅰ）程序框图如下：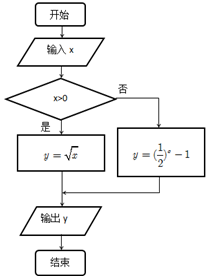

（Ⅱ） 由程序可得y=$\left\{\begin{array}{l}{\sqrt{x}}&{x＞0}\\{（\frac{1}{2}）^{x}-1}&{x≤0}\end{array}\right.$，
∵y＞1，
∴①当x≤0时，${（\frac{1}{2}）^x}-1＞1$，
即2^-x＞2，
∴-x＞1，
∴x＜-1．
②当x＞0时，$\sqrt{x}$＞1，
即x＞1，
故输入的x值的范围为（-∞，-1）∪（1，+∞）．

点评 本题考查了画出程序框图的问题，解题时应分析程序语言，把程序语言转化为程序框图，考查了画图的能力和分类讨论思想，是基础题．