
已知 、
、 、
、 为正实数,
为正实数, .
.
(1)当 、
、 、
、 为
为 的三边长,且
的三边长,且 、
、 、
、 所对的角分别为
所对的角分别为 、
、 、
、 .若
.若 ,且
,且 .求
.求 的长;
的长;
(2)若 .试证明长为
.试证明长为 、
、 、
、 的线段能构成三角形,而且边
的线段能构成三角形,而且边 的对角为
的对角为 .
.
(1)2;(2)见解析.
解析试题分析:(1)本题属于解三角形问题,它是“已知两边及一边所对的角,求第三边”的问题,解决这个问题可以有两种方法,一种是先用正弦定理求出已知两边所对的角中未知的一角,从而可求得第三角,然后用余弦定理求出第三边,也可以直接用余弦定理列出待求边的方程,通过解方程求出第三边;(2)首先要证明长为 、
、 、
、 的线段能构成三角形,即证
的线段能构成三角形,即证 ,即证
,即证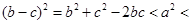
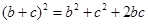 ,而这个不等式通过已知条件,再利用
,而这个不等式通过已知条件,再利用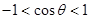 易得,其次再由余弦定理很快可得
易得,其次再由余弦定理很快可得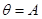 .
.
试题解析:(1)解:由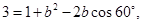
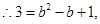 (3分)
(3分) (5分)
(5分)
(2)证:由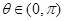 ,可得
,可得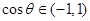 (6分)
(6分)
所以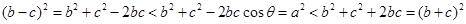
也就是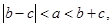 (9分)
(9分)
因此长为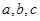 的线段能构成三角形,不妨记为
的线段能构成三角形,不妨记为 。
。
在  中,由余弦定理可设
中,由余弦定理可设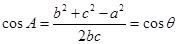 (11分)
(11分)
即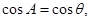 又
又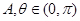 ,由
,由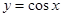 的单调性可得
的单调性可得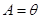 (14分)
(14分)
所以边 的对角为
的对角为 .
.
考点:(1)余弦定理;(2)三条线段构成三角形的条件.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
△ABC中,角A,B,C的对边分别为a,b,c,已知sinAsinB+sinBsinC+cos2B=1.
(1)求证:a,b,c成等差数列;(2)若C=
 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知m= ,n=
,n= ,满足
,满足 .
.
(1)将y表示为x的函数 ,并求
,并求 的最小正周期;
的最小正周期;
(2)已知a,b,c分别为 ABC的三个内角A,B,C对应的边长,
ABC的三个内角A,B,C对应的边长, 的最大值是
的最大值是 ,且a=2,求b+c的取值范围.
,且a=2,求b+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c,且cos(A-B)cosB-sin(A-B)sin(A+C)
=- .
.
(1)求sinA的值;
(2)若a=4 ,b=5,求向量
,b=5,求向量 在
在 方向上的投影.
方向上的投影.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,a、b、c分别为角A、B、C的对边,若m=(sin2 ,1),n="(-2,cos" 2A+1),且m⊥n.
,1),n="(-2,cos" 2A+1),且m⊥n.
(1)求角A的度数;
(2)当a=2 ,且△ABC的面积S=
,且△ABC的面积S= 时,求边c的值和△ABC的面积.
时,求边c的值和△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com