
已知 为偶函数,曲线
为偶函数,曲线 过点
过点 ,
,  .
.
(1)若曲线 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围;
的取值范围;
(2)若当 时函数
时函数 取得极值,确定
取得极值,确定 的单调区间.
的单调区间.
(1)  ;(2)
;(2)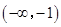 和
和 为
为 的单调递增区间,
的单调递增区间, 为
为 的单调递增区间.
的单调递增区间.
解析试题分析:(1)先根据 为偶函数,得到
为偶函数,得到 ,恒有
,恒有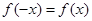 ,进而计算出
,进而计算出 (也可根据二次函数的图像与性质得到对称轴
(也可根据二次函数的图像与性质得到对称轴 ,该对称轴为
,该对称轴为 轴,进而得出
轴,进而得出 ),然后将点
),然后将点 代入求出
代入求出 ,进而写出
,进而写出 的表达式,此时
的表达式,此时 ,根据条件
,根据条件 有斜率为0的切线即
有斜率为0的切线即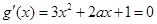 有实数解,根据二次方程有解的条件可得
有实数解,根据二次方程有解的条件可得 ,求解出
,求解出 的取值范围即可;(2)先根据
的取值范围即可;(2)先根据 时函数
时函数 取得极值,得到
取得极值,得到 ,进而求出
,进而求出 ,然后确定导函数
,然后确定导函数 ,由导数
,由导数 可求出函数的单调增区间,由
可求出函数的单调增区间,由 可求出函数的单调减区间.
可求出函数的单调减区间.
(1)  为偶函数,故对
为偶函数,故对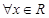 ,总有
,总有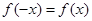 ,易得
,易得
又曲线 过点
过点 ,得
,得 ,得
,得 ,
, 3分
3分
 曲线
曲线 有斜率为0的切线,故
有斜率为0的切线,故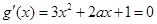 有实数解
有实数解
此时有 ,解得
,解得 5分
5分
(2)因 时函数
时函数 取得极值,故有
取得极值,故有 ,解得
,解得
又 ,令
,令 ,得
,得 .
.
当 时,
时,
 在
在 上为增函数
上为增函数
当 时,
时, ,
, 在
在 上为减函数
上为减函数
当 时,
时, ,
, 在
在 上为增函数
上为增函数
从而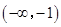 和
和 为
为 的单调递增区间,
的单调递增区间, 为
为 的单调递增区间 10分.
的单调递增区间 10分.
考点:1.函数的奇偶性;2.导数的几何意义;3.函数的极值与导数;4.函数的单调性与导数.


科目:高中数学 来源: 题型:解答题
(本题满分14分)本题有2个小题,第一小题满分6分,第二小题满分1分.
设常数 ,函数
,函数
若 =4,求函数
=4,求函数 的反函数
的反函数 ;
;
根据 的不同取值,讨论函数
的不同取值,讨论函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=x+ 的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).
的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).
(1)求g(x)的解析式;
(2)若直线y=m与C2只有一个交点,求m的值和交点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设f(x)是(-∞,+∞)上的奇函数,f(x+2)=-f(x),
当0≤x≤1时,f(x)=x.
(1)求f(3)的值;
(2)当-4≤x≤4时,求f(x)的图像与x轴所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某幼儿园准备建一个转盘,转盘的外围是一个周长为k米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连经预算,转盘上的每个座位与支点相连的钢管的费用为3k元/根,且当两相邻的座位之间的圆弧长为x米时,相邻两座位之间的钢管和其中一个座位的总费用为 k元.假设座位等距分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记转盘的总造价为y元.
k元.假设座位等距分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记转盘的总造价为y元.
(1)试写出y关于x的函数关系式,并写出定义域;
(2)当k=50米时,试确定座位的个数,使得总造价最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com