
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 将函数进行化简,结合三角函数的图象和性质依次判断命题的对错即可得到答案.
解答 解:由f(x)=cos2x-2$\sqrt{3}$sinxcosx,
?f(x)=cos2x-$\sqrt{3}$sin2x
?f(x)=2sin(2x$+\frac{π}{6}$)
f(x)的周期T=$\frac{2π}{2}=π$,则有f(x1)=f(π+x1),
∴当x1-x2=π时,f(x1)=f(x2)成立.故①对.
由sinx函数的图象和性质,可得:f(x)的单调递增区间为[kπ-$\frac{2π}{3}$,$kπ+\frac{π}{6}$],(k∈Z),
区间[-$\frac{π}{6}$,$\frac{π}{3}}$]?[kπ-$\frac{2π}{3}$,$kπ+\frac{π}{6}$],k∈Z,故②不对.
函数f(x)的图象的中心对称为($\frac{kπ}{2}-\frac{π}{12}$,0),(k∈Z),经考查($\frac{π}{12}$,0)不是对称中心.故③不对.
由f(x)=2sin(2x$+\frac{π}{6}$)向左平移$\frac{5π}{12}$个单位后得到:2sin[2(x+$\frac{5π}{12}$)+$\frac{π}{6}$]⇒化简得:-2sin2x,与y=2sin2x的图象不重合.故④不对.
综上所述:①对,②③④不对.
故选:A
点评 本题考查了三角函数的化简能力和计算能力,以及三角函数的图象和性质的运用能力.综合性比较强,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
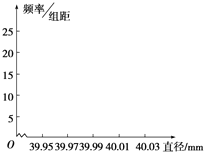 某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:
某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:| 分组 | 频数 | 频率 | $\frac{频率}{组距}$ |
| [39.95,39.97) | 2 | 0.10 | 5 |
| [39.97,39.99) | 4 | 0.20 | 10 |
| [39.99,40.01) | 10 | 0.50 | 25 |
| [40.01,40.03] | 4 | 0.20 | 10 |
| 合计 | 20 | 1 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{2})$ | B. | (-∞,-1) | C. | ($\frac{1}{2}$,+∞) | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日销售量 | 1 | 1.5 | 2 |
| 天数 | 10 | 25 | 15 |
| 频率 | 0.2 | a | b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(2)<2f(3) | B. | 2f(3)<3f(2) | C. | 3f(4)<4f(3) | D. | 2f(3)<3f(4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com