
 甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,用茎叶图表示这两组数据.
甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,用茎叶图表示这两组数据. =
=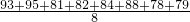 =85,
=85, =
=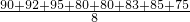 =85,
=85,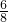 =
= .
. ).
).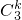 (
(  )k(
)k(  )3-k,k=0,1,2,3.
)3-k,k=0,1,2,3.| ξ | 0 | 1 | 2 | 3 |
| P |  |  |  |  |
 +1×
+1× +2×
+2× +3×
+3× =
= …12分
…12分 =
= ,s乙2<s甲2,所以乙的成绩较稳定,因此派乙参赛比较合适.
,s乙2<s甲2,所以乙的成绩较稳定,因此派乙参赛比较合适. 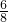 ,随机变量ξ 的可能取值为0、1、2、3,由题意可得ξ服从二项分布,即ξ~B(3,
,随机变量ξ 的可能取值为0、1、2、3,由题意可得ξ服从二项分布,即ξ~B(3, ),进而根据公式即可得到分布列与期望.
),进而根据公式即可得到分布列与期望.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com