练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    一次考试中，要求考生从试卷上的9个题目中选6个进行答题，要求至少包含前5个题目中的3个，则考生答题的不同选法的种数是  ________．


    　74


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    小王参加一次比赛，比赛共设三关，第一、二关各有两个必答题，如果每关两个问题都答对，可进入下一关，第三关有三个问题，只要答对其中两个问题，则闯关成功．每过一关可一次性获得价值分别为1 000元，3 000元，6 000元的奖品(不重复得奖)，小王对三关中每个问题回答正确的概率依次为，，，且每个问题回答正确与否相互独立．

    (1)求小王过第一关但未过第二关的概率；

    (2)用X表示小王所获得奖品的价值，写出X的概率分布列，并求X的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    小波以游戏方式决定是参加学校合唱团还是参加学校排球队．游戏规则为：以O为起点，再从A1，A2，A3，A4，A5，A6，A7，A8(如图)这8个点中任取两点分别为终点得到两个向量，记这两个向量的数量积为X.若X＝0就参加学校合唱团，否则就参加学校排球队．

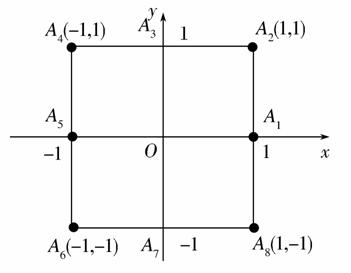
    (1)求小波参加学校合唱团的概率；

    (2)求X的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


               .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    从1，3，5，7，9这五个数中，每次取出两个不同的数分别记为a，b，共可得到lg a－lg b的不同值的个数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在图1中，“构建和谐社会，创美好未来”，从上往下读(不能跳读)，共有不同的读法种数是________．

    构

    建　建

    和　和　和

    谐　谐　谐　谐

    社　社　社　社　社

    会　会　会　会　会　会

    创　创　创　创　创

    美　美　美　美

    好　好　好

    未　未

    来

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数 的定义域是（　　）

        A．（-  ,1）     B．（-  ,+∞）   C．（-  , ）           D．(-∞,- )

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知复数z满足z•i=2﹣i，i为虚数单位，则z的共轭复数为（　　）

    　

    A．

    ﹣1+2 i

    B．

    l+2i

    C．

    2﹣i

    D．

    ﹣1﹣2i

    查看答案和解析>>

    科目：高中数学 来源： 题型：


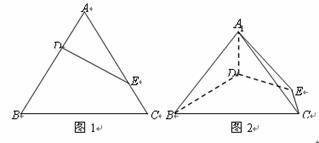
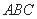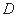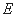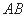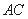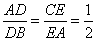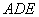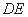    等边三角形的边长为3,点、分别是边、上的点,且满足 (如图1)．将△沿折起到△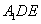的位置,使二面角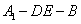为直二面角,连结 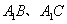(如图2)．

    （Ⅰ）求证: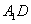平面；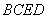

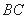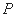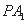    （Ⅱ）在线段上是否存在点,使直线与平面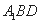所成的角为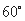?若存在,求出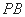的长,若不存在,请说明理由．

    查看答案和解析>>

    同步练习册答案