
等边三角形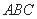 的边长为3,点
的边长为3,点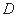 、
、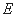 分别是边
分别是边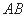 、
、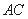 上的点,且满足
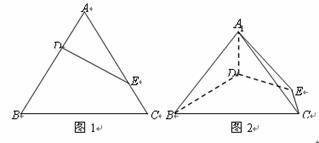
上的点,且满足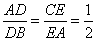 (如图1).将△
(如图1).将△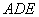 沿
沿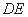 折起到△
折起到△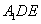 的位置,使二面角
的位置,使二面角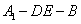 为直二面角,连结
为直二面角,连结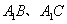 (如图2).
(如图2).
(Ⅰ)求证: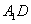
 平面
平面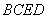 ;
;
(Ⅱ)在线段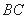 上是否存在点
上是否存在点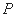 ,使直线
,使直线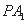 与平面
与平面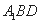 所成的角为
所成的角为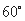 ?若存在,求出
?若存在,求出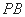 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
(1)因为等边△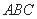 的边长为3,且
的边长为3,且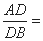
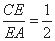 ,
,
所以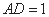 ,
,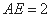 . 在△
. 在△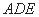 中,
中,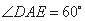 ,
,
由余弦定理得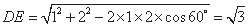 . 因为
. 因为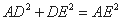 ,
,
所以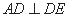 .……………3分
.……………3分
折叠后有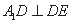 ,因为二面角
,因为二面角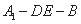 是直二面角,
是直二面角,
所以平面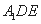
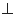 平面
平面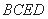 ,又平面
,又平面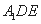
 平面
平面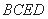
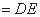 ,
,
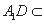 平面
平面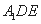 ,
,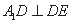 , 所以
, 所以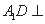 平面
平面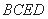 .………6分
.………6分
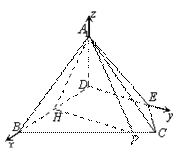
(2)解法1:假设在线段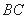 上存在点
上存在点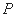 ,使直线
,使直线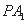 与平面
与平面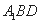 所成的角为
所成的角为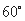 .
.
如图,作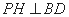 于点
于点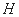 ,连结
,连结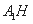 、
、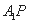 ,
,
由(1)有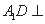 平面
平面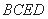 ,而
,而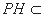 平面
平面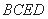 ,
,
所以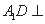
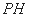 ,又
,又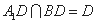 , 所以
, 所以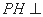 平面
平面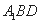 ,
,
所以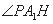 是直线
是直线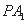 与平面
与平面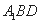 所成的角 , ………………………8分
所成的角 , ………………………8分
设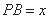
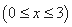 ,则
,则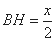 ,
, ,
,
在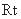 △
△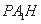 中,
中,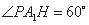 ,所以
,所以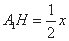 ,
,
在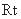 △
△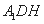 中,
中,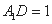 ,
,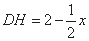 ,
,
由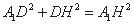 , 得
, 得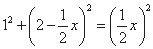 ,解得
,解得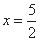 ,满足
,满足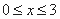 ,符合题意
,符合题意
所以在线段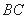 上存在点
上存在点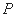 ,使直线
,使直线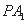 与平面
与平面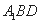 所成的角为
所成的角为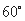 ,此时
,此时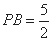 ………12分
………12分
解法2:由(1)的证明,可知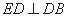 ,
,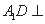 平面
平面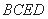 .
.
以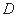 为坐标原点,以射线
为坐标原点,以射线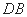 、
、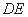 、
、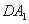 分别为
分别为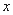 轴、
轴、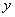 轴、
轴、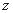 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系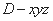 如图 ,设
如图 ,设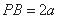
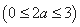 , 则
, 则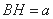 ,
,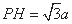 ,
,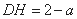 ,
,
所以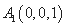 ,
,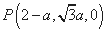 ,
,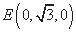 ,所以
,所以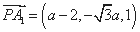 ,
,
因为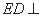 平面
平面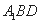 , 所以平面
, 所以平面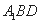 的一个法向量为
的一个法向量为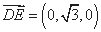 , ………………………9分
, ………………………9分
因为直线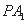 与平面
与平面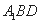 所成的角为
所成的角为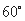 , 所以
, 所以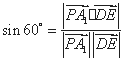 ,
,
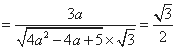 , 解得
, 解得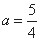 ,
,
即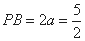 ,满足
,满足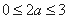 ,符合题意,
,符合题意,
所以在线段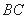 上存在点
上存在点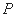 ,使直线
,使直线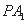 与平面
与平面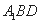 所成的角为
所成的角为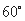 ,此时
,此时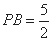 .………12分
.………12分


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
为了解大学生身体素质情况,从某大学共800名男生中随机抽取50人测量身高。 据测量,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组 ;第二组
;第二组 ;…;第八组
;…;第八组 .如图是按上述分组方法得到的频率分布直方图.
.如图是按上述分组方法得到的频率分布直方图.
(1)估计这所学校高三年级全体男生身高在180cm以上 (含180cm)的人数;
(2)若从身高属于第六组和第八组的所有男生中随机抽
取两人,记他们的身高分别为 ,求满足“
,求满足“ ”的事件的概率.
”的事件的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com