
分析 (1)利用椭圆上的点到焦点距离的最大值为2+$\sqrt{3}$,最小值为2-$\sqrt{3}$,由此可求a,c然后求解b,即可得到椭圆T的方程;
(2)直线方程与椭圆方程联立,利用韦达定理求出|PQ|,求出原点到直线l的距离,表示出三角形的面积,进而利用基本不等式,即可求得△OPQ面积的最大值.
解答 解:(1)由题意:椭圆上的点到焦点距离的最大值为2+$\sqrt{3}$,最小值为2-$\sqrt{3}$,
则:a+c=2+$\sqrt{3}$,a-c=2-$\sqrt{3}$,解得a=2,c=$\sqrt{3}$,b=1.
故所求椭圆方程为$\frac{{x}^{2}}{4}$+y2=1.
(2)联立$\left\{\begin{array}{l}{y=kx+\sqrt{3}}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,整理得(1+4k2)x2+8$\sqrt{3}$kx+8=0,
令P(x1,y1),Q(x2,y2),则x1+x2=$\frac{-8\sqrt{3}k}{1+4{k}^{2}}$,x1x2=$\frac{8}{1+4{k}^{2}}$,
△=(8$\sqrt{3}$k)2-32(1+4k2)>0,即:2k2-1>0,
又原点到直线l的距离为d=$\frac{\sqrt{3}}{\sqrt{1+{k}^{2}}}$,|PQ|=$\sqrt{1+{k}^{2}}$|x1-x2|,
∴S△OPQ=$\frac{1}{2}$|PQ|•d=$\frac{\sqrt{3}}{2}$|x1-x2|=$\frac{\sqrt{3}}{2}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=2$\sqrt{6}$•$\sqrt{\frac{2{k}^{2}-1}{(1+4{k}^{2})^{2}}}$
=2$\sqrt{6}$•$\sqrt{\frac{2{k}^{2}-1}{4(2{k}^{2}-1)^{2}+12(2{k}^{2}-1)+9}}$
=2$\sqrt{6}$•$\sqrt{\frac{1}{4(2{k}^{2}-1)+\frac{9}{2{k}^{2}-1}+12}}$
≤$2\sqrt{6}×\sqrt{\frac{1}{24}}$=1当且仅当k=$\frac{\sqrt{5}}{2}$时取等号,
则△OPQ面积的最大值为1.
点评 本题考查椭圆的标准方程,考查直线与圆相切,考查三角形面积的计算,考查基本不等式的运用,正确表示三角形的面积是关键.


科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
选修4—1:几何证明选讲
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.
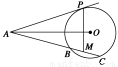
(1) 证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:选择题
已知函数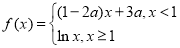 的值域为
的值域为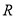 ,那么
,那么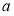 的取值范围是( )
的取值范围是( )
A. 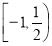 B.
B.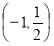 C.(-∞,-1] D.
C.(-∞,-1] D.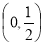
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
已知函数
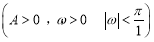 的部分图象如图所示,下列说法正确的是( )
的部分图象如图所示,下列说法正确的是( )
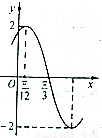
A.函数 的最小正周期为
的最小正周期为
B.函数 的图象关于点
的图象关于点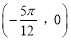 对称
对称
C.将函数 的图象向左平移
的图象向左平移 个单位得到的函数图象关于
个单位得到的函数图象关于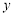 轴对称
轴对称
D.函数 的单调递增区间是
的单调递增区间是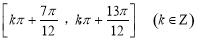
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,AD为∠BAC的平分线,AE为边BC上的中线,已知AB=3,AC=5,AE=$\frac{7}{2}$.
如图,在△ABC中,AD为∠BAC的平分线,AE为边BC上的中线,已知AB=3,AC=5,AE=$\frac{7}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
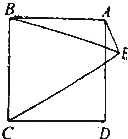 如图,若点E为正方形ABCD外一点,∠BEC=45°,连AE.
如图,若点E为正方形ABCD外一点,∠BEC=45°,连AE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com