
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
分析 (Ⅰ)根据题目中的数表求出需要志愿者提供帮助的老年人的比例估计值;
(Ⅱ)根据列联表计算观测值,对照临界值表即可得出结论;
(Ⅲ)按分层抽样求出抽取的男性、女性人数,利用列举法求出基本事件数,再计算对应的概率值.
解答 解:(Ⅰ)根据题目中的数表得,
调查的500位老年人中有70位需要志愿者提供帮助,
因此该地区老年人中,需要志愿者提供帮助的老年人的比例的估计值为
$\frac{70}{500}=14$%;
(Ⅱ)根据列联表,计算观测值$K_{\;}^2=\frac{{500×(40×270-30×160)_{\;}^2}}{200×300×70×430}≈9.967>6.635$,
对照临界值表知,有99%的把握认为该地区的老年人是否需要帮助与性别有关;
(Ⅲ)按分层抽样抽取7人,男性有4人,可记为A、B、C、D,女性3人,可记为e、f、g,
现从7人中抽取2人,基本事件是AB、AC、AD、Ae、Af、Ag、BC、BD、Be、Bf、Bg、
CD、Ce、Cf、Cg、De、Df、Dg、ef、eg、fg共21种不同的方法,
恰是一男一女的有Ae、Af、Ag、Be、Bf、Bg、Ce、Cf、Cg、De、Df、Dg共12种不同的方法,
故所求的概率为P=$\frac{12}{21}$=$\frac{4}{7}$.
点评 本题考查了独立性检验的应用问题,也考查了利用列举法求古典概型的概率问题,是基础题目.


科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
已知c>0,设命题p:函数 为减函数.命题q:当
为减函数.命题q:当 时,函数f(x)=x+
时,函数f(x)=x+ >
> 恒成立.如果“p∨q”为真命题,“p∧q”为假命题,求c的取值范围.
恒成立.如果“p∨q”为真命题,“p∧q”为假命题,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:解答题
已知函数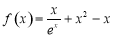 (其中
(其中 ).
).
(1)求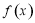 在
在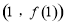 处的切线方程;
处的切线方程;
(2)已知函数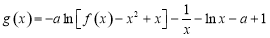 ,若
,若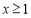 ,则
,则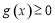 ,求实数
,求实数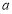 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
设向量 与
与 满足
满足 ,
, 在
在 方向上的投影为1,若存在实数
方向上的投影为1,若存在实数 ,使得
,使得 与
与 垂直,则
垂直,则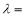 ( )
( )
A.3 B.2 C.1 D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,300] | >300 |
| 空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 重度污染 |
| 天数 | 6 | 14 | 18 | 27 | 20 | 15 |
| 非严重污染 | 严重污染 | 合计 | |
| 供暖季 | 22 | 8 | 30 |
| 非供暖季 | 63 | 7 | 70 |
| 合计 | 85 | 15 | 100 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
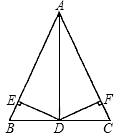 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF,则图中全等的三角形有( )对.
如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF,则图中全等的三角形有( )对.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com