
分析 (1)不等式即|2x-1|-|x-1|>1,转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求;
(2)由题意可得,当x∈(-2,1)时,|x-1|+|x-a|>|2x-a-1|=|(x-a)+(x-1)|恒成立,可得(x-a)与(x-1)的符号相反,从而求得a的范围.
解答 解:(1)∵f(x)=|x-a|,当a=1时,不等式f(x)<|2x-1|-1,
即|2x-1|-|x-1|>1,
∴$\left\{\begin{array}{l}{x<\frac{1}{2}}\\{1-2x-(1-x)>1}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{\frac{1}{2}≤x≤1}\\{2x-1-(1-x)>1}\end{array}\right.$②,或 $\left\{\begin{array}{l}{x>1}\\{2x-1-(x-1)>1}\end{array}\right.$ ③.
解①求得x<-1,解②求得x∈∅,解③求得x>1.
综上可得,不等式的解集为{x|x<-1,或x>1}.
(2)∵当x∈(-2,1)时,|x-1|>|2x-a-1|-f(x),
即|x-1|+|x-a|>|2x-a-1|=|(x-a)+(x-1)|恒成立.
∴(x-a)与(x-1)的符号相反,
即x-a 与1-x的符号相同,∴a≤-2.
点评 本题主要考查绝对值不等式的解法,绝对值三角不等式的应用,属于中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:选择题
已知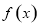 是以2为周期的偶函数,当
是以2为周期的偶函数,当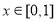 时,
时,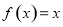 ,且在[-1,3]内,关于
,且在[-1,3]内,关于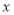 的方程
的方程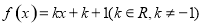 有四个根,则
有四个根,则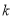 的取值范围是( )
的取值范围是( )
A.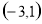 B.
B.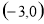 C.
C.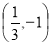 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
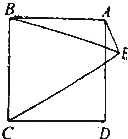 如图,若点E为正方形ABCD外一点,∠BEC=45°,连AE.
如图,若点E为正方形ABCD外一点,∠BEC=45°,连AE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,D是△ABC中边BC上一点,AD=AB,记∠CAD=α,∠ABC=β,sinα+cos2β=0,若AC=$\sqrt{3}$DC,求β的值.
如图,D是△ABC中边BC上一点,AD=AB,记∠CAD=α,∠ABC=β,sinα+cos2β=0,若AC=$\sqrt{3}$DC,求β的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com