
分析 (1)求出圆心到切线的距离得半径,代入圆的标准方程得答案;
(2)由题意画出图形,数形结合得答案.
解答 解:(1)由r=$\frac{|1×(-2)+1×0-4|}{\sqrt{2}}=3\sqrt{2}$,又圆心C(-2,0),
得圆C的方程为(x+2)2+y2=18;
(2)如图,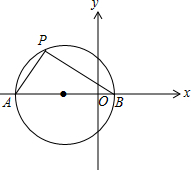
对于圆C上的动点P(x,y),恒有PA2+PB2=72,
则A,B分别为圆与x轴的左右交点,
在(x+2)2+y2=18中,取y=0,得${x}_{1}=-2-3\sqrt{2},{x}_{2}=-2+3\sqrt{2}$,
∴$a=-2-3\sqrt{2},b=-2+3\sqrt{2}$.
点评 本题考查直线与圆的位置关系的应用,考查了数形结合的解题思想方法,是中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:解答题
已知函数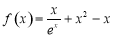 (其中
(其中 ).
).
(1)求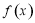 在
在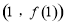 处的切线方程;
处的切线方程;
(2)已知函数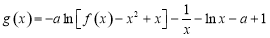 ,若
,若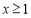 ,则
,则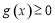 ,求实数
,求实数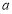 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
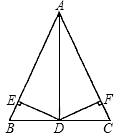 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF,则图中全等的三角形有( )对.
如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF,则图中全等的三角形有( )对.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com