
分析 (1)由递推公式求出a2,a3的值,由作差法得到$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{2(n+1)}{n+2}$,再根据累乘法求出数列的通项公式,
(Ⅱ)由题意存在n∈N*,且n≥2,使得$\frac{{a}_{n}}{{2}^{n}•λ}$≥$\frac{3n}{n-1}$成立,转化为存在n∈N*,且n≥2,使λ≤$\frac{n-1}{2n(n+1)}$成立,设bn=$\frac{n-1}{2n(n+1)}$,n≥2,判断出数列的单调性,求出数列的最大值,即可求出λ的范围,问题得以解决.
解答 解:(Ⅰ)由2a1+3a2+…+nan-1=(n+1)an,
当n=2时,得到2a1=3a2,即a2=2,
当n=3时,得到2a1+3a2=4a3,即a3=3,
∵2a1+3a2+…+nan-1=(n+1)an,①,
∴2a1+3a2+…+nan-1+(n+1)an=(n+2)an+1,②,
②-①,得
(n+1)an=(n+2)an+1-(n+1)an,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{2(n+1)}{n+2}$
∴$\frac{{a}_{2}}{{a}_{1}}$×$\frac{{a}_{3}}{{a}_{2}}$×$\frac{{a}_{4}}{{a}_{3}}$×…×$\frac{{a}_{n}}{{a}_{n-1}}$=2n-2×($\frac{2}{3}$×$\frac{3}{4}$×$\frac{4}{5}$×…×$\frac{n}{n+1}$)=$\frac{{2}^{n-1}}{n+1}$,
∴an=3×$\frac{{2}^{n-1}}{n+1}$,
当n=1时,a1不成立,
故an=$\left\{\begin{array}{l}{3,n=1}\\{3×\frac{{2}^{n-1}}{n+1},n≥2}\end{array}\right.$
(Ⅱ)存在n∈N*,且n≥2,使得$\frac{{a}_{n}}{{2}^{n}•λ}$≥$\frac{3n}{n-1}$成立,
∴$\frac{3×\frac{{2}^{n-1}}{n+1}}{{2}^{n}•λ}$≥$\frac{3n}{n-1}$,
即λ≤$\frac{n-1}{2n(n+1)}$,
设bn=$\frac{n-1}{2n(n+1)}$,n≥2,
则bn+1-bn=$\frac{n}{2(n+1)(n+2)}$-$\frac{n-1}{2n(n+1)}$=$\frac{2-n}{2n(n+1)(n+2)}$,
当n≥2时,数列{bn}为递减数列,
故当n=2时,bn有最大值,即为b2=$\frac{1}{12}$,
∴λ≤$\frac{1}{12}$,
故正实数λ的最大值为$\frac{1}{12}$
点评 本题考查了数列的递推公式和数列的通项公式的求法,以及存在性的问题,考查了作差法累乘法,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
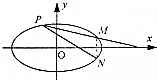 在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且右准线方程为x=4.
在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且右准线方程为x=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | 1 | C. | $\frac{9}{5}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{7}{4}$ | C. | -$\frac{7}{4}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com