
| A. | $\frac{1}{5}$ | B. | 1 | C. | $\frac{9}{5}$ | D. | $\frac{8}{9}$ |
分析 当AB是圆的切线时,∠OAB最大,当AB经过圆心时∠OAB最小且等于0°.而当A点距圆心O越近时,∠OAB的最大值越大;A距圆心越远时,∠OAB的最大值越小.只要使∠OAB的最大值不小于45°就行了,也就是要找到使∠OAB的最大值等于45°的极限点A,当∠OAB=45°时,连接OB,就得到一个∠OAB=45°的三角形,这时OA=$\sqrt{2}$OB,则A的坐标满足:(x-0)2+(y-0)2=2 与x+2y-3=0,求解方程组可得答案.
解答 解:设点A(x,y)如图,当AB是圆的切线时,∠OAB最大,
∠OAB=45°时,连接OB,就得到一个∠OAB=30°的Rt三角形,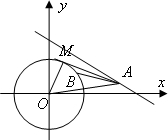
这时OA=$\sqrt{2}$OB,圆O的半径是1,那么只要求出在直线I上距圆心为$\sqrt{2}$的点的横坐标,即可求得点A的横坐标的最大值.
点A的坐标满足:(x-0)2+(y-0)2=2 与x+2y-3=0,
解得x=$\frac{1}{5}$或x=1.
∴点A的横坐标的最大值为1.
故选:B.
点评 本题主要考查直线与圆的位置关系的判断,以及转化与化归的思想方法.正确理解题意是解答该题的关键,是中档题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
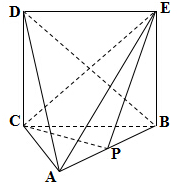 如图所示,△ABC中,AC=1,AB=2,∠ACB=$\frac{π}{2}$,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.
如图所示,△ABC中,AC=1,AB=2,∠ACB=$\frac{π}{2}$,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,+∞) | B. | (-∞,9) | C. | [3,+∞) | D. | [8,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 4$\sqrt{2}$+2 | C. | 4$\sqrt{2}$-2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从身高在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取6人参加一项活动,再从这6人选两人当正负队长,则这两人体重不在同一组内的概率为$\frac{11}{15}$.
从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从身高在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取6人参加一项活动,再从这6人选两人当正负队长,则这两人体重不在同一组内的概率为$\frac{11}{15}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com