
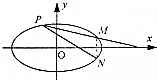
 在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且右准线方程为x=4.
在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且右准线方程为x=4.分析 (1)由椭圆的离心率为$\frac{1}{2}$,且右准线方程为x=4,列方程组解得a=2,c=1,由此能求出椭圆的标准方程.
(2)由P(x1,y1),M(x2,y2),得N(x2,-y2),求出直线PM的方程和直线PN的方程,分别令y=0,得m和n,由此能推导出m•n为定值.
解答 解:(1)由题意,得$\frac{c}{a}=\frac{1}{2}$,且$\frac{{a}^{2}}{c}=4$,
解得a=2,c=1,
∴$b=\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴椭圆的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)由P(x1,y1),M(x2,y2),得N(x2,-y2),
∴$\frac{{{x}_{1}}^{2}}{4}$+$\frac{{{y}_{1}}^{2}}{3}$=1,$\frac{{{x}_{2}}^{2}}{4}+\frac{{{y}_{2}}^{2}}{3}=1$,
直线PM的方程为y-y1=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}(x-{x}_{1})$,
直线PN的方程为y-y1=$\frac{-{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$(x-x1),
分别令y=0,得m=$\frac{{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{y}_{2}-{y}_{1}}$,n=$\frac{{x}_{1}{y}_{2}+{x}_{2}{y}_{1}}{{y}_{2}+{y}_{1}}$,
∴mn=$\frac{{{x}_{1}}^{2}{{y}_{2}}^{2}-{{x}_{2}}^{2}{{y}_{1}}^{2}}{{y}_{2}-{y}_{1}}$=$\frac{(4-\frac{4}{3}{{y}_{1}}^{2}){{y}_{2}}^{2}-(4-\frac{4}{3}{{y}_{2}}^{2}){{y}_{1}}^{2}}{{{y}_{2}}^{2}-{{y}_{1}}^{2}}$=$\frac{4({{y}_{2}}^{2}-{{y}_{1}}^{2})}{{{y}_{2}}^{2}-{{y}_{1}}^{2}}$=4为定值,
∴m•n为定值4.
点评 本题考查椭圆方程的求法,考查两数值是否为定值的判断与求法,是中档题,解题时要认真审题,注意直线与椭圆性质的合理运用.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:选择题
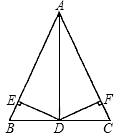 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF,则图中全等的三角形有( )对.
如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF,则图中全等的三角形有( )对.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
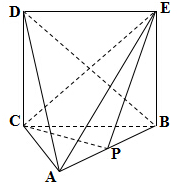 如图所示,△ABC中,AC=1,AB=2,∠ACB=$\frac{π}{2}$,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.
如图所示,△ABC中,AC=1,AB=2,∠ACB=$\frac{π}{2}$,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com