
分析 (1)求导数,确定切线的斜率,即可求函数f(x)在点(${\frac{π}{2}$,f(${\frac{π}{2}}$))处的切线方程;
(2)由f'(x)=-xsinx=0,x>0,得${x_n}=nπ({n∈{N^*}})$,所以当n≥2且n∈N*时,$\frac{1}{x_n^2}=\frac{1}{{{n^2}{π^2}}}<\frac{1}{{({n-1})({n+1}){π^2}}}=\frac{1}{{2{π^2}}}({\frac{1}{{({n-1})}}-\frac{1}{{({n+1})}}})$.利用放缩法,即可证明结论.
解答 (1)解:f'(x)=cosx-xsinx-cosx=-xsinx,则切线的斜率为$f'({\frac{π}{2}})=-\frac{π}{2}sin\frac{π}{2}=-\frac{π}{2}$,
又$f({\frac{π}{2}})=-1$,故函数f(x)在点$({\frac{π}{2},f({\frac{π}{2}})})$处的切线方程为$y-({-1})=-\frac{π}{2}({x-\frac{π}{2}})$,即$\frac{π}{2}x+y+1-\frac{π^2}{4}=0$.
(2)证明:由f'(x)=-xsinx=0,x>0,得${x_n}=nπ({n∈{N^*}})$,
所以当n≥2且n∈N*时,$\frac{1}{x_n^2}=\frac{1}{{{n^2}{π^2}}}<\frac{1}{{({n-1})({n+1}){π^2}}}=\frac{1}{{2{π^2}}}({\frac{1}{{({n-1})}}-\frac{1}{{({n+1})}}})$.
所以当n≥2时,n∈N*时,$\frac{1}{x_1^2}+\frac{1}{x_2^2}+\frac{1}{x_3^2}+…+\frac{1}{x_n^2}<\frac{1}{π^2}+\frac{1}{{2{π^2}}}$$({1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{n-3}-\frac{1}{n-1}+\frac{1}{n-2}-\frac{1}{n}+\frac{1}{n-1}-\frac{1}{n+1}})$=$\frac{1}{π^2}+\frac{1}{{2{π^2}}}({1+\frac{1}{2}-\frac{1}{n}-\frac{1}{n+1}})<\frac{1}{π^2}+\frac{1}{{2{π^2}}}({1+\frac{1}{2}})=\frac{7}{{4{π^2}}}$.
又当n=1时,$\frac{1}{x_1^2}=\frac{1}{π^2}<\frac{7}{{4{π^2}}}$.
综上,$\frac{1}{x_1^2}+\frac{1}{x_2^2}+\frac{1}{x_3^2}+…+\frac{1}{x_n^2}<\frac{7}{{4{π^2}}}({n∈{N^*}})$.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
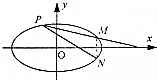 在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且右准线方程为x=4.
在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,且右准线方程为x=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{7}{4}$ | C. | -$\frac{7}{4}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com