
分析 利用分子有理化的方法,先化简,再进行大小比较.
解答 解:(1)$\sqrt{12}$-$\sqrt{11}$=$\frac{1}{\sqrt{12}+\sqrt{11}}$,$\sqrt{11}$-$\sqrt{10}$=$\frac{1}{\sqrt{11}+\sqrt{10}}$,
∵$\sqrt{12}$+$\sqrt{11}$>$\sqrt{11}$+$\sqrt{10}$,
∴$\frac{1}{\sqrt{12}+\sqrt{11}}$<$\frac{1}{\sqrt{11}+\sqrt{10}}$,
∴$\sqrt{12}$-$\sqrt{11}$>$\sqrt{11}$-$\sqrt{10}$;
(2)2$\sqrt{2}$-$\sqrt{6}$=$\frac{2}{2\sqrt{2}+\sqrt{6}}$.
∵2$\sqrt{2}$+$\sqrt{6}$<$\sqrt{6}$+4,
∴$\frac{2}{2\sqrt{2}+\sqrt{6}}$>$\frac{2}{\sqrt{6}+4}$,
∴$\frac{2}{\sqrt{6}+4}$<2$\sqrt{2}$-$\sqrt{6}$.
点评 本题考查大小比较,考查学生的计算能力,正确分子有理化是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
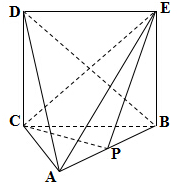 如图所示,△ABC中,AC=1,AB=2,∠ACB=$\frac{π}{2}$,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.
如图所示,△ABC中,AC=1,AB=2,∠ACB=$\frac{π}{2}$,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从身高在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取6人参加一项活动,再从这6人选两人当正负队长,则这两人体重不在同一组内的概率为$\frac{11}{15}$.
从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从身高在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取6人参加一项活动,再从这6人选两人当正负队长,则这两人体重不在同一组内的概率为$\frac{11}{15}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$π | B. | $\frac{28}{3}$π | C. | 3π | D. | $\frac{4}{3}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com