
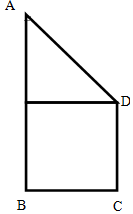
 已知四边形ABCD为直角梯形,AB∥CD,AB=4,BC=CD=2,AB⊥BC,现将该梯形绕AB所在直线旋转一周,得到一个封闭的几何体,求该几何体的表面积及体积.
已知四边形ABCD为直角梯形,AB∥CD,AB=4,BC=CD=2,AB⊥BC,现将该梯形绕AB所在直线旋转一周,得到一个封闭的几何体,求该几何体的表面积及体积. 分析 通过已知条件知道,绕AB旋转一周形成的封闭几何体是上面是圆锥,下面是圆柱的图形.所以该几何体的表面积便是圆锥、圆柱的表面积和底面圆的面积的和,该几何体的体积便是圆锥、圆柱体积的和,所以根据已知的边的长度及圆锥、圆柱的表面积公式,及体积公式即可求出该几何体的表面积和体积.
解答 解:依题旋转后形成的几何体为上部为圆锥,下部为圆柱的图形,如下图所示:
其表面积S=圆锥侧面积+圆柱侧面积+圆柱底面积;
∴S=4$\sqrt{2}$π+8π+4π=12π+4$\sqrt{2}$π;
其体积V=圆锥体积+圆柱体积;
∴V=$\frac{8}{3}$π+8π=$\frac{32}{3}$π.
点评 考查对由平面图形绕一直线旋转之后形成的立体图形的判断,以及圆锥、圆柱的表面积公式,体积公式.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数的极大值就是函数的最大值 | |
| B. | 函数的极小值就是函数的最小值 | |
| C. | 函数的最值一定是极值 | |
| D. | 闭区间上的连续函数一定存在最大值与最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{9}{16}$ | C. | $\frac{9}{16}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com