
| 2 |
| 3 |
| 2 |
| 3 |
| 7-3 |
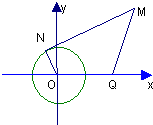 解:(1)如图,设MN切圆于N,则动点M组成的集合是P={M||MN|=λ|MQ|},式中常数λ>0.
解:(1)如图,设MN切圆于N,则动点M组成的集合是P={M||MN|=λ|MQ|},式中常数λ>0.| x2+y2-1 |
| (x-2)2+y2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 2λ2 |
| λ2-1 |
| 1+3λ2 |
| (λ2-1)2 |
| 2λ2 |
| λ2-1 |
| ||
| |λ2-1| |
| 2 |
| 3 |
| 7-3 |
| 3 |
| 4 |
| |12+5a-4| |
| 5 |
| 18 |
| 5 |
| 2 |
| 5 |


科目:高中数学 来源: 题型:
| A、已知a、b为异面直线,过空间中不在a、b上的任意一点,可以作一个平面与a、b都平行 | ||
| B、在二面角α-l-β的两个半平面α、β内分别有直线a、b,则二面角α-l-β是直二面角的充要条件是α⊥β或b⊥a | ||
C、已知异面直线a与b成60°,分别在a、b上的线段AB与CD的长分别为4和2,AC、BD 的中点分别为E、F,则EF=
| ||
D、正三棱锥的内切球的半径为1,则此正三棱锥的体积最小值8
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1+a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| y2 |
| a2 |
| x2 |
| b2 |
| NA |
| AF |
| NB |
| BF |
查看答案和解析>>
科目:高中数学 来源: 题型:
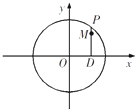 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=| 4 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com