练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．集合P={x，1}，Q={y，1，2}，其中x，y∈{1，2，3，…，9}，且P⊆Q．把满足上述条件的一对有序整数对（x，y）作为一个点的坐标，则这样的点的个数是（　　）
    A．14B．21C．9D．15

    分析 根据题意，由集合包含的意义，分析可得若P⊆Q，有2种情况：①、x≠y，则必有x=2，②、x=y，分析x、y可取的值，即可得每种情况中（x，y）的情况数目，由分类计数原理，将其相加计算可得答案．

    解答 解：根据题意，若P⊆Q，有2种情况：
    ①、x≠y，则必有x=2，y可取的值为3、4、5、6、7、8、9，共7种情况，即（x，y）有7种情况，
    ②、x=y，此时x、y可取的值为3、4、5、6、7、8、9，共7种情况，即（x，y）有7种情况，
    则（x，y）有7+7=14种情况，
    故选：A．

    点评 本题考查分类计数原理的运用，关键是由集合中包含关系的定义，分析得到x、y可取的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．若直线x+y=2与曲线（x-4）2+y2=a2（a＞0）有且只有一个公共点，则a的值为（　　）
    A．1B．$\sqrt{2}$C．2D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

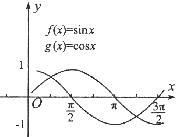    20．如图所示，由函数f（x）=sinx与函数g（x）=cosx在区间$[{0，\frac{3π}{2}}]$上的图象所围成的封闭图形的面积为2$\sqrt{2}$-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．在平行四边形ABCD中，$\overrightarrow{AB}$=（2，4），$\overrightarrow{AC}$=（1，3），求平行四边形ABCD的面积2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．为调查某地区老人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：
    性别
    是否需要志愿者    		男女
    需要4030
    不需要160270
    由K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$算得K2=$\frac{{500×{{（40×270-30×160）}^2}}}{200×300×70×430}$=9.967
    附表：
    P（K2≥k）0.0500.0100.001
    k3.8416.63510.828
    参照附表，则下列结论正确的是（　　）
    ①有99%以上的把握认为“该地区的老年人是否需要志愿者提供帮助与性别无关”；
    ②有99%以上的把握认为“该地区的老年人是否需要志愿者提供帮助与性别有关”；
    ③采用系统抽样方法比采用简单随机抽样方法更好；
    ④采用分层抽样方法比采用简单随机抽样方法更好．
    A．①③B．①④C．②③D．②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．设F是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{24}$=1的右焦点且椭圆上至少有25个不同的点Pi（i=1，2，3，…），|P1F|，|P2F|，|P3F|，…组成公差为d的等差数列，则实数d的取值范围是[-$\frac{1}{12}$，0）∪（0，$\frac{1}{12}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．设定义在（0，+∞）上的单调函数f（x），对任意的x∈（0，+∞）都有f[f（x）-log2x]=6，若x0是方程f（x）+f（x-2）=10的一个解，且x0∈（a，a+1）（a∈N*），则a=（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

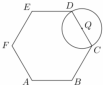    18．如图，在边长为2的正六边形ABCDEF中，动圆⊙Q的半径为1，圆心在线段CD（含端点）上运动，P为⊙Q上及内部的动点，设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AF}$（m，n∈R），则m+n的取值范围是[2，5]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．以直角坐标系的原点为极点，x轴的正半轴为极轴，已知曲线C1、C2的极坐标方程分别为$θ=0，θ=\frac{π}{3}$，曲线C3的参数方程为$\left\{{\begin{array}{l}{x=2cosα}\\{y=2sinα}\end{array}}\right.$（α为参数，且$α∈[{-\frac{π}{2}，\frac{π}{2}}]$），则曲线C1、C2、C3所围成的封闭图形的面积是$\frac{2}{3}$π．

    查看答案和解析>>

    同步练习册答案