练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．在平行四边形ABCD中，$\overrightarrow{AB}$=（2，4），$\overrightarrow{AC}$=（1，3），求平行四边形ABCD的面积2．

    分析 利用数量积公式求出A的余弦值，进一步求出正弦值，利用平行四边形的面积公式求之．

    解答 解：由题意cosA=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}=\frac{14}{\sqrt{20}•\sqrt{10}}=\frac{7}{5\sqrt{2}}$，所以sinA=$\frac{1}{5\sqrt{2}}$，所以平行四边形的面积为$|\overrightarrow{AC}|sinA•|\overrightarrow{AB}|$=$\sqrt{20}×\frac{1}{5\sqrt{2}}×\sqrt{10}=2$；
    故答案为：2．

    点评 本题考查了平面向量的数量积公式的运用；关键是利用数量积求出A的正弦值，从而求出平行四边形的高．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．求值${∫}_{2}^{4}$（$\frac{1}{x}$+x）dx=ln2+6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．一个空心球玩具里面设计一个棱长为4的内接正四面体，过正四面体上某一个顶点所在的三条棱的中点作球的截面，则该截面圆的面积是$\frac{16π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知直线l：y=-ex+a与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b≥0）有一个公共点M，e为椭圆的离心率，直线l与x轴和y轴的交点分别为A、B，且$\overrightarrow{AM}$=λ$\overrightarrow{AB}$．
    （Ⅰ）若点A（$\frac{4\sqrt{3}}{3}$，0）、B（0，2），求椭圆方程；
    （II）若e=$\frac{1}{3}$，求λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t+1}\end{array}\right.$（t为参数），曲线C的参数方程为$\left\{\begin{array}{l}{x=2+cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数）
    （1）以原点O为极点，以x轴正半轴为极轴（与直角坐标系xOy取相同的长度单位）建立极坐标系，若点P的极坐标为（4，$\frac{π}{3}$），判断点P与直线l的位置关系；
    （2）设点Q是曲线C上的一个动点，利用曲线C的参数方程求Q到直线l的距离的最大值与最小值的差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．对长期吃含三聚氰胺的婴幼儿奶粉与患肾结石这两个分类变量的计算中，下列说法正确的是（　　）
    A．若Χ2的值大于6.635，我们有99%的把握认为长期吃含三聚氰胺的婴幼儿奶粉与患肾结石有关系，那么在1000个长期吃含三聚氰胺的婴幼儿奶粉的婴幼儿中必有999人患有肾结石病
    B．从独立性检验可知有99%的把握认为吃含三聚氰胺的婴幼儿奶粉与患肾结石有关系时，我们说某一个婴幼儿吃含三聚氰胺的婴幼儿奶粉，那么他有99%的可能患肾结石病
    C．若从统计量中求出有95%的把握认为吃含三聚氰胺的婴幼儿奶粉与患肾结石病有关系，是指有5%的可能性使得推断出现错误
    D．以上三种说法都不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．集合P={x，1}，Q={y，1，2}，其中x，y∈{1，2，3，…，9}，且P⊆Q．把满足上述条件的一对有序整数对（x，y）作为一个点的坐标，则这样的点的个数是（　　）
    A．14B．21C．9D．15

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．早上从起床到出门需要洗脸刷牙（5min）、刷水壶（2min）、烧水（8min）、泡面（3min）、吃饭（10min）、听广播（8min）几个步骤．从下列选项中选出最好的一种流程（　　）
    A．1．洗脸刷牙、2．刷水壶、3．烧水、4．泡面、5．吃饭、6．听广播
    B．1．刷水壶、2．烧水同时洗脸刷牙、3．泡面、4．吃饭、5．听广播
    C．1．刷水壶、2．烧水同时洗脸刷牙、3．泡面、4．吃饭同时听广播
    D．1．吃饭同时听广播、2．泡面、3．烧水同时洗脸刷牙、4．刷水壶

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

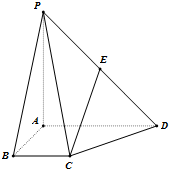    7．如图，在梯形ABCD中，BC∥AD，AB⊥BC，AB=BC=1，PA=AD=2，PA⊥平面ABCD，E为PD中点．
    （Ⅰ）求证：CE∥平面PAB；
    （Ⅱ）求直线CE与平面PAD所成角的大小．

    查看答案和解析>>

    同步练习册答案