
分析 棱长为4的内接正四面体的高为$\sqrt{16-(\frac{4\sqrt{3}}{3})^{2}}$=$\frac{4\sqrt{6}}{3}$,外接球的半径$\sqrt{6}$,求出球心到截面的距离,可得截面圆的半径,即可求出截面圆的面积.
解答 解:棱长为4的内接正四面体的高为$\sqrt{16-(\frac{4\sqrt{3}}{3})^{2}}$=$\frac{4\sqrt{6}}{3}$,外接球的半径$\sqrt{6}$,
∴过正四面体上某一个顶点所在的三条棱的中点作球的截面,球心到截面的距离d=$\frac{\sqrt{6}}{3}$,
∴截面圆的半径为$\sqrt{6-(\frac{\sqrt{6}}{3})^{2}}$=$\frac{4\sqrt{3}}{3}$,
∴截面圆的面积是4πr2=$\frac{16π}{3}$.
故答案为:$\frac{16π}{3}$.
点评 本题考查截面圆的面积,考查学生的计算能力,确定截面圆的半径是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
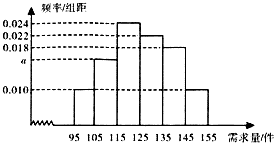 某商场经销某一种电器商品,在一个销售季度内,每售出一件该电器商品获利200元,未售出的商品,每一件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示.现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件,95≤n≤155)表示下一个销售季度内市场需求量,Y(单位:元)表示下一个销售季度内销售该
某商场经销某一种电器商品,在一个销售季度内,每售出一件该电器商品获利200元,未售出的商品,每一件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示.现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件,95≤n≤155)表示下一个销售季度内市场需求量,Y(单位:元)表示下一个销售季度内销售该查看答案和解析>>
科目:高中数学 来源: 题型:填空题
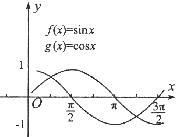 如图所示,由函数f(x)=sinx与函数g(x)=cosx在区间$[{0,\frac{3π}{2}}]$上的图象所围成的封闭图形的面积为2$\sqrt{2}$-1.
如图所示,由函数f(x)=sinx与函数g(x)=cosx在区间$[{0,\frac{3π}{2}}]$上的图象所围成的封闭图形的面积为2$\sqrt{2}$-1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
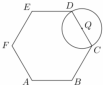 如图,在边长为2的正六边形ABCDEF中,动圆⊙Q的半径为1,圆心在线段CD(含端点)上运动,P为⊙Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AF}$(m,n∈R),则m+n的取值范围是[2,5].
如图,在边长为2的正六边形ABCDEF中,动圆⊙Q的半径为1,圆心在线段CD(含端点)上运动,P为⊙Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AF}$(m,n∈R),则m+n的取值范围是[2,5].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com