
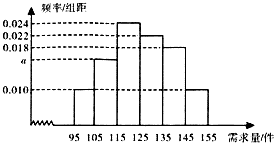
 某商场经销某一种电器商品,在一个销售季度内,每售出一件该电器商品获利200元,未售出的商品,每一件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示.现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件,95≤n≤155)表示下一个销售季度内市场需求量,Y(单位:元)表示下一个销售季度内销售该
某商场经销某一种电器商品,在一个销售季度内,每售出一件该电器商品获利200元,未售出的商品,每一件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示.现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件,95≤n≤155)表示下一个销售季度内市场需求量,Y(单位:元)表示下一个销售季度内销售该分析 (Ⅰ)根据分段函数的定义写出函数的表达式即可;
(Ⅱ)根据小长方形的面积之和等于1即可求出a的值;
(Ⅲ)根据分段函数求出n≥115件,即可求出P(n≥115)的概率.
解答 解:(Ⅰ)依题意知下一个销售季度内销售该电器的利润Y与需求量n之间的关系为
Y=$\left\{\begin{array}{l}{200n-100(125-n),95≤n≤125}\\{125×200,126≤n≤155}\end{array}\right.$,
(Ⅱ)由(0.010×2+a+0.018+0.022+0.024)×10=1,
求得a=0.016,
(Ⅲ)而300n-100×125≥22000,知n≥115件,
∴P(n≥115)=1-0.1-0.16=0.74
点评 本题考查频率分布直方图,概率的求法,找出利润与需求量之间的关系是解决本题的关键,属于中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-2,2) | C. | [-1,2) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若Χ2的值大于6.635,我们有99%的把握认为长期吃含三聚氰胺的婴幼儿奶粉与患肾结石有关系,那么在1000个长期吃含三聚氰胺的婴幼儿奶粉的婴幼儿中必有999人患有肾结石病 | |
| B. | 从独立性检验可知有99%的把握认为吃含三聚氰胺的婴幼儿奶粉与患肾结石有关系时,我们说某一个婴幼儿吃含三聚氰胺的婴幼儿奶粉,那么他有99%的可能患肾结石病 | |
| C. | 若从统计量中求出有95%的把握认为吃含三聚氰胺的婴幼儿奶粉与患肾结石病有关系,是指有5%的可能性使得推断出现错误 | |
| D. | 以上三种说法都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com