练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知集合A={x|x2+x+1=0}，B={x|-2≤x＜2}，则（∁RA）∩B=（　　）
    A．[-1，1]B．[-2，2）C．[-1，2）D．∅

    分析 分别求出A的解集，求出A补集与B的交集即可．

    解答 解：A={x|x2+x+1=0}=∅，
    ∴∁RA=R，
    B={x|-2≤x＜2}=[-2，2），
    则∁RA∩B=[-2，2）
    故选：B．

    点评 此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．已知（1+ax）5 的展开式中x2的系数为40，则a=（　　）
    A．±1B．±2C．2D．-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知单位向量使得$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$的夹角为120°，点使得A（-2，0），B（0，3），若$\overline{AB}={e_1}+k{e_2}$，则k的值为（　　）
    A．3或4B．3或-4C．-3或4D．-3或-4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．定义2×2矩阵$[\begin{array}{l}{a_1}\\{a_3}\end{array}\right.\left.\begin{array}{l}{a_2}\\{a_4}\end{array}]={a_1}{a_4}-{a_2}{a_3}$，若$f（x）=[{\begin{array}{l}{{{cos}^2}x-{{sin}^2}x}&{\sqrt{3}}\\{cos（\frac{π}{2}+2x）}&1\end{array}}]$，则f（x）（　　）
    A．图象关于（π，0）中心对称B．图象关于直线$x=\frac{π}{2}$对称
    C．在区间$[-\frac{π}{6}，0]$上单调递增D．周期为π的奇函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

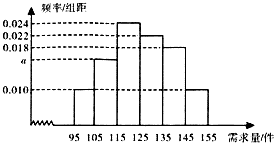    13．某商场经销某一种电器商品，在一个销售季度内，每售出一件该电器商品获利200元，未售出的商品，每一件亏损100元，根据以往资料，得到销售季度内市场需求量的频率分布直方图，如图所示．现在经销商为下一个销售季度购进了125件该种电器，以n（单位：件，95≤n≤155）表示下一个销售季度内市场需求量，Y（单位：元）表示下一个销售季度内销售该
    电器的利润．
    （I）将Y表示为n的函数；
    （Ⅱ）求频率分布直方图中n的值；
    （Ⅲ）根据直方图估计利润Y不少于22000元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．某校准备从报名的7位教师（其中男教师4人，女教师3人）中选3人去边区支教．
    （Ⅰ）设所选 3人中女教师的人数为X，求X的分布列及数学期望；
    （Ⅱ）若选派的三人依次到甲、乙、丙三个地方支教，求甲地是男教师的情况下，乙地为女教师的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．为研究大气污染与人的呼吸系统疾病是否有关，对重污染地区和轻污染地区做跟踪调查，得出如下资料：
    患呼吸系
    统疾病    		未患呼吸
    系统疾病    		总计
    重污染地区10313971500
    轻污染地区1314871500
    总计11628843000
    根据列联表，求得K2的值为72.636．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知a=tan50°，b=1+cos20°，c=2sin160°，则这三个数的大小关系为（　　）
    A．b＜c＜aB．a＜b＜cC．c＜a＜bD．c＜b＜a

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．在极坐标系中，已知曲线C的方程为$ρ=\frac{4cosθ}{{{{sin}^2}θ}}$，直线l的直角坐标方程为x-y+1=0，则直线l与曲线C的位置关系为（　　）
    A．相交B．相切C．相离D．不能确定

    查看答案和解析>>

    同步练习册答案