
分析 根据题意画出图形,结合图形利用平面向量的线性表示与运算性质,即可求出x+y的值.
解答 解:如图所示,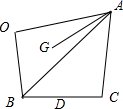
G为△AOB的重心,
∴$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AO}$+$\overrightarrow{AB}$)=$\frac{1}{3}$($\overrightarrow{AO}$+$\overrightarrow{OB}$-$\overrightarrow{OA}$)=-$\frac{2}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$,
又$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,且$\overrightarrow{AG}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,
∴x=-$\frac{2}{3}$,y=$\frac{1}{3}$,
∴x+y=-$\frac{1}{3}$.
故答案为:-$\frac{1}{3}$.
点评 本题考查了平面向量的线性表示与运算问题,是基础题目.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:解答题
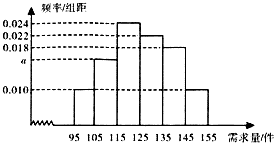 某商场经销某一种电器商品,在一个销售季度内,每售出一件该电器商品获利200元,未售出的商品,每一件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示.现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件,95≤n≤155)表示下一个销售季度内市场需求量,Y(单位:元)表示下一个销售季度内销售该
某商场经销某一种电器商品,在一个销售季度内,每售出一件该电器商品获利200元,未售出的商品,每一件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示.现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件,95≤n≤155)表示下一个销售季度内市场需求量,Y(单位:元)表示下一个销售季度内销售该查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
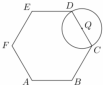 如图,在边长为2的正六边形ABCDEF中,动圆⊙Q的半径为1,圆心在线段CD(含端点)上运动,P为⊙Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AF}$(m,n∈R),则m+n的取值范围是[2,5].
如图,在边长为2的正六边形ABCDEF中,动圆⊙Q的半径为1,圆心在线段CD(含端点)上运动,P为⊙Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AF}$(m,n∈R),则m+n的取值范围是[2,5].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
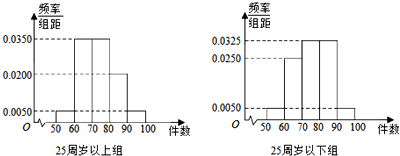
| 生产能手 | 非生产能手 | 合计 | |
| 25周岁以上组 | 15 | 45 | 60 |
| 25周岁以下组 | 15 | 25 | 40 |
| 合计 | 30 | 70 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com