
分析 (1)由题意的离心率得到a,b的关系,把椭圆方程化为x2+3y2=3b2.设出M,A的坐标,代入椭圆方程得到M,A两点横纵坐标的关系,把直线MA,MB的斜率用两点坐标表示,作积后得答案;
(2)由已知求得椭圆方程,设出直线AB的方程,联立直线方程和椭圆方程,化为关于x的一元二次方程,由k1+k2=3得到直线AB的斜率和截距的关系,再由直线系方程得到直线AB过定点的坐标.
解答 (1)解:由$e=\frac{c}{a}=\frac{\sqrt{6}}{3}$,得$\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{2}{3}$,∴a2=3b2,
设椭圆方程为x2+3y2=3b2.
再设M(x0,y0),A(x1,y1),则B(-x1,-y1),
则有${{x}_{0}}^{2}+3{{y}_{0}}^{2}=3{b}^{2}$,${{x}_{1}}^{2}+3{{y}_{1}}^{2}=3{b}^{2}$,
${k}_{1}{k}_{2}=\frac{{y}_{0}-{y}_{1}}{{x}_{0}-{x}_{1}}•\frac{{y}_{0}+{y}_{1}}{{x}_{0}+{x}_{1}}=\frac{{{y}_{0}}^{2}-{{y}_{1}}^{2}}{{{x}_{0}}^{2}-{{x}_{1}}^{2}}$=$\frac{{{y}_{0}}^{2}-{{y}_{1}}^{2}}{3({{y}_{0}}^{2}-{{y}_{1}}^{2})}=-\frac{1}{3}$;
(2)证明:M(0,1),则b2=1,∴椭圆方程为x2+3y2=3.
设AB方程:y=kx+m,设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{{x}^{2}+3{y}^{2}=3}\\{y=kx+m}\end{array}\right.$,得(1+3k2)x2+6kmx+3m2-3=0.
△=36k2m2-(4+12k2)(3m2-3)=12(3k2-m2+1)>0.
${x}_{1}+{x}_{2}=\frac{-6km}{1+3{k}^{2}},{x}_{1}{x}_{2}=\frac{3{m}^{2}-3}{1+3{k}^{2}}$,
${k}_{1}+{k}_{2}=\frac{{y}_{1}-1}{{x}_{1}}+\frac{{y}_{2}-1}{{x}_{2}}=\frac{2k{x}_{1}{x}_{2}+(m+1)({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}=3$.
则$\frac{2k•\frac{3{m}^{2}-3}{1+3{k}^{2}}+(m+1)•\frac{-6km}{1+3{k}^{2}}}{\frac{3{m}^{2}-3}{1+3{k}^{2}}}=3$,整理得3m2-3=2km-2k,即3m+3=2k,
∴y=kx+$\frac{2}{3}k-1$,则直线过定点(-$\frac{2}{3}$,-1).
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,考查“设而不求”的解题思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若Χ2的值大于6.635,我们有99%的把握认为长期吃含三聚氰胺的婴幼儿奶粉与患肾结石有关系,那么在1000个长期吃含三聚氰胺的婴幼儿奶粉的婴幼儿中必有999人患有肾结石病 | |
| B. | 从独立性检验可知有99%的把握认为吃含三聚氰胺的婴幼儿奶粉与患肾结石有关系时,我们说某一个婴幼儿吃含三聚氰胺的婴幼儿奶粉,那么他有99%的可能患肾结石病 | |
| C. | 若从统计量中求出有95%的把握认为吃含三聚氰胺的婴幼儿奶粉与患肾结石病有关系,是指有5%的可能性使得推断出现错误 | |
| D. | 以上三种说法都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
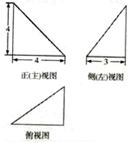
| A. | 28 | B. | 24+6$\sqrt{2}$ | C. | 20+2$\sqrt{13}$ | D. | 16+6$\sqrt{2}$+2$\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1.洗脸刷牙、2.刷水壶、3.烧水、4.泡面、5.吃饭、6.听广播 | |
| B. | 1.刷水壶、2.烧水同时洗脸刷牙、3.泡面、4.吃饭、5.听广播 | |
| C. | 1.刷水壶、2.烧水同时洗脸刷牙、3.泡面、4.吃饭同时听广播 | |
| D. | 1.吃饭同时听广播、2.泡面、3.烧水同时洗脸刷牙、4.刷水壶 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 重心 | B. | 内心 | C. | 外心 | D. | 垂心 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com