
分析 (1)由题已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3及其夹角,可利用$|\overrightarrow{a}|=\sqrt{|\overrightarrow{a}{|}^{2}}$,转化为向量的乘法解决;
(2)求向量$\overrightarrow{a}$+2$\overrightarrow{b}$在$\overrightarrow{b}$方向上的投影,则由向量乘法$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>$,则$\overrightarrow{a}$在$\overrightarrow{b}$的投影为|$\overrightarrow{a}$|cos$<\overrightarrow{a},\overrightarrow{b}>$,则可利用|$\overrightarrow{a}$|cos$<\overrightarrow{a},\overrightarrow{b}>$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$变形.可求出投影.
解答 解:(1)∵|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,
∴|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{|\overrightarrow{a}+2\overrightarrow{b}{|}^{2}}=\sqrt{(\overrightarrow{a}+2\overrightarrow{b})^{2}}$=$\sqrt{|\overrightarrow{a}{|}^{2}+4\overrightarrow{a}•\overrightarrow{b}+4|\overrightarrow{b}{|}^{2}}$
=$\sqrt{4+4|\overrightarrow{a}||\overrightarrow{b}|cos120°+4×9}$=$\sqrt{40+4×2×3×(-\frac{1}{2})}$=2$\sqrt{7}$;
(2)∵$(\overrightarrow{a}+2\overrightarrow{b})•\overrightarrow{b}$=$\overrightarrow{a}•\overrightarrow{b}+2|\overrightarrow{b}{|}^{2}=|\overrightarrow{a}||\overrightarrow{b}|cos120°+18$=$2×3×(-\frac{1}{2})+18=15$,
∴$\overrightarrow{a}$+2$\overrightarrow{b}$在$\overrightarrow{b}$方向上的投影为|$\overrightarrow{a}+2\overrightarrow{b}$|•cos<$\overrightarrow{a}+2\overrightarrow{b}$,$\overrightarrow{b}$>=$\frac{(\overrightarrow{a}+2\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{15}{3}=5$.
点评 本题考查平面向量的数量积运算,考查了向量在向量方向上投影的概念,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 中国鞋码实际标注(同国标码)mm | 220 | 225 | 230 | 235 | 240 | 245 | 250 | 255 | 260 | 265 |
| 中国鞋码习惯叫法(同欧码) | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
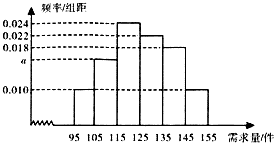 某商场经销某一种电器商品,在一个销售季度内,每售出一件该电器商品获利200元,未售出的商品,每一件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示.现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件,95≤n≤155)表示下一个销售季度内市场需求量,Y(单位:元)表示下一个销售季度内销售该
某商场经销某一种电器商品,在一个销售季度内,每售出一件该电器商品获利200元,未售出的商品,每一件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示.现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件,95≤n≤155)表示下一个销售季度内市场需求量,Y(单位:元)表示下一个销售季度内销售该查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com