
分析 (1)将P的极坐标(4,$\frac{π}{3}$),转化成直角坐标P(2,2$\sqrt{3}$),将参数方程转化成直角坐标,由P点坐标不满足直线l的方程,P不在直线l上;
(2)将C的参数方程转化成直角坐标方程,取得圆心坐标及半径,由点到直线记得距离公式求得圆心到直线的距离d,即可求得点Q到直线l的距离的最小值为d-r和最大值为d+r,两式相减即可求得结果.
解答 解:(1)把点P的极坐标(4,$\frac{π}{3}$),转化成直角坐标P(2,2$\sqrt{3}$),
把直线l的参数方程:$\left\{\begin{array}{l}{x=\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t+1}\end{array}\right.$,化为直角坐标方程为y=$\sqrt{3}$x+1,
由于点P的坐标不满足直线l的方程,故P不在直线l上,
(2)点Q是曲线C上的一个动点,曲线C的参数方程为$\left\{\begin{array}{l}{x=2+cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),
曲线C的直角坐标方程为:(x-2)2+y2=1,
∴曲线C表示已(2,0)为圆心,1为半径的圆,
圆心到直线的距离为d=$\frac{丨2\sqrt{3}-0+1丨}{\sqrt{3+1}}$=$\sqrt{3}$+$\frac{1}{2}$,
故点Q到直线l的距离的最小值为d-r=$\sqrt{3}$-$\frac{1}{2}$,
最大值为d+r=$\sqrt{3}$+$\frac{3}{2}$,
∴曲线C的参数方程求Q到直线l的距离的最大值与最小值的差2.
点评 本题考查点的极坐标化为直角坐标,参数方程转化成直角坐标方程,直线与圆的位置关系,点到直线的距离公式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
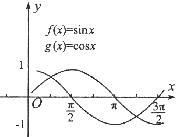 如图所示,由函数f(x)=sinx与函数g(x)=cosx在区间$[{0,\frac{3π}{2}}]$上的图象所围成的封闭图形的面积为2$\sqrt{2}$-1.
如图所示,由函数f(x)=sinx与函数g(x)=cosx在区间$[{0,\frac{3π}{2}}]$上的图象所围成的封闭图形的面积为2$\sqrt{2}$-1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com