Question

甲、乙、丙三人按下面的规则进行乒乓球比赛：第一局由甲、乙参加而丙轮空，
以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为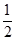，且各局胜负相互独立.求：
（1）打满3局比赛还未停止的概率；
（2）比赛停止时已打局数的分别列与期望E.

Answer 1

（1）；（2）分布列　

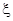
	2	3	4	5	6
P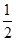

 
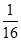
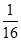
从而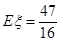（局）.

解析试题分析：（1）首先用字母表示事件:如令分别表示甲、乙、丙在第k局中获胜,由于打满3局比赛还未停止，即在三局比赛中没有人连胜两局，分析其可能情况知为事件，每局比赛的结果相互独立且互斥，利用独立事件、互斥事件的概率求解即可．（2）先写出ξ的所有可能值为2，3，4，5，6，ξ＝2的含义是:甲连胜两局或乙连胜两局,故得,同理可分别求出ξ取每一个值的概率，列出分布列即可，再利用数学期望公式：求出的数学期望．
试题解析：令分别表示甲、乙、丙在第k局中获胜.
（1）由独立事件同时发生与互斥事件至少有一个发生的概率公式知，打满3局比赛还未停止的概率为
（2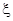）的所有可能值为2，3，4，5，6，且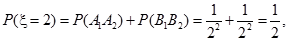　




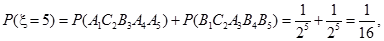
故有分布列

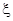
	2	3	4	5	6
P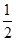

 
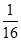
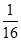
从而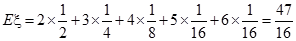（局）.
考点：１．互斥、独立事件的概率；２．离散型随机变量的分布列和期望．