
在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,记ξ=|x-2|+|y-x|.
(1)求随机变量ξ的最大值,并求事件“ξ取得最大值”的概率;
(2)求随机变量ξ的分布列.
(1)3,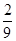 ;(2)见解析
;(2)见解析
解析试题分析:(1)通过分析x,y的取值情况,先求出|x-2|与|y-x|的最大值,从而求出ξ的最大值,分析ξ取最大值时,x,y的取值情况及x,y所有取值情况,根据古典概型公式求出所求事件的概率;(2)先分析ξ的所有可能取值及取该值时x,y的取值情况,根据古典概型公式求出分布列.
试题解析:(1)∵x,y可能的取值为1,2,3,
∴|x-2|≤1,|y-x|≤2,
∴ξ≤3,且当x=1,y=3或x=3,y=1时,ξ=3.
因此,随机变量ξ的最大值为3.(3分)
∵有放回抽两张卡片的所有情况有3×3=9种,
∴P(ξ=3)=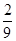 .
.
故随机变量ξ的最大值为3,事件“ξ取得最大值”的概率为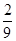 .(6分)
.(6分)
(2)ξ的所有取值为0,1,2,3.
∵ξ=0时,只有x=2,y=2这一种情况,
ξ=1时,有x=1,y=1或x=2,y=1或x=2,y=3或x=3,y=3四种情况,
ξ=2时,有x=1,y=2或x=3,y=2两种情况.
ξ=3时,有x=1,y=3或x=3,y=1两种情况.
∴P(ξ=0)= ,P(ξ=1)=
,P(ξ=1)=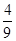 ,P(ξ=2)=
,P(ξ=2)=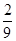 ,
,
P(ξ=3)=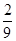 .(10分)
.(10分)
则随机变量ξ的分布列为:ξ 0 1 2 3 P 
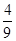
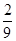
考点:古典概型,分类整合思想


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个.
(Ⅰ)从中同时摸出两个球,求两球颜色恰好相同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为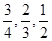 ,乙队每人答对的概率都是
,乙队每人答对的概率都是 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用 表示甲队总得分.
表示甲队总得分.
(I)求随机变量 的分布列及其数学期望E
的分布列及其数学期望E ;
;
(Ⅱ)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,
以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为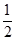 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求:
(1)打满3局比赛还未停止的概率;
(2)比赛停止时已打局数 的分别列与期望E
的分别列与期望E .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次任意抽取3道题,独立作答,然后由乙回答剩余3题,每人答对其中的2题就停止答题,即闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 .
.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.(1)求甲、乙两人考试均合格的概率;(2)求甲答对试题数 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种玫瑰花,进货商当天以每支1元从鲜花批发商店购进,以每支2元售出.若当天卖不完,剩余的玫瑰花批发商店以每支0.5元的价格回收.根据市场统计,得到这个季节的日销售量X(单位:支)的频率分布直方图(如图所示),将频率视为概率.(12分)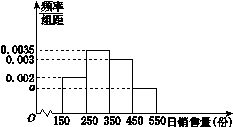
(1)求频率分布直方图中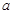 的值;
的值;
(2)若进货量为 (单位支),当n≥X时,求利润Y的表达式;
(单位支),当n≥X时,求利润Y的表达式;
(3)若当天进货量n=400,求利润Y的分布列和数学期望E(Y)(统计方法中,同一组数据常用该组区间的中点值作为代表).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com