
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() 平面
平面![]() .
.
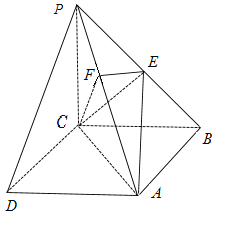
(Ⅰ)求证:![]() 为
为![]() 的中点;
的中点;
(Ⅱ)当![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)证明见详解;(Ⅱ)![]()
【解析】
(Ⅰ)利用线面平行的性质定理可得![]() ,再根据三角形的中位线性质即可证出.
,再根据三角形的中位线性质即可证出.
(Ⅱ)首先作出线面角,利用三角形的面积相等可得![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,求出平面
轴,建立空间直角坐标系,求出平面![]() 的一个法向量与平面
的一个法向量与平面![]() 的一个法向量,利用空间向量的数量积即可求解.
的一个法向量,利用空间向量的数量积即可求解.
(Ⅰ)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,
平面![]() 平面
平面![]()
![]() ,
,
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
则![]() ,
,
![]() 底面
底面![]() 是正方形,点
是正方形,点![]() 为
为![]() 的中点,
的中点,
![]()
![]() 为
为![]() 的中点.
的中点.
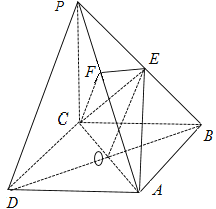
(Ⅱ)由底面![]() 是正方形,且
是正方形,且![]() ,则
,则![]() ,
,
又![]() 底面
底面![]() ,所以
,所以![]() ,
,
又![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
在平面![]() 内,过
内,过![]() 作
作![]() ,连接
,连接![]() ,
,
则![]() 与平面
与平面![]() 所成的角
所成的角![]() 最大.
最大.
设![]() ,则
,则![]() ,
,
由![]() ,即
,即![]() ,解得
,解得![]() ,
,
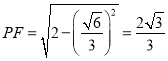 ,即
,即![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,
建立空间直角坐标系,如图:
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则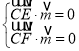 ,即
,即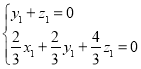 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,、
,、
设平面![]() 的一个法向量
的一个法向量![]() ,
,
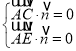 ,即
,即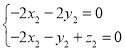 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
所以![]()
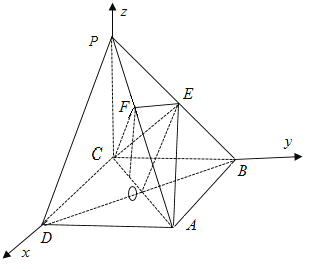
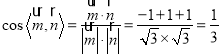 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
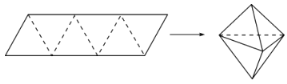
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽粒,古称角黍,是端午节大家都会品尝的食品.如图,平行四边形形状的纸片是由六个边长为2的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为_________;若该六面体内有一球,当该球体积最大时,球的表面积是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们生活水平的不断提高,肥胖人数不断增多.世界卫生组织(WHO)常用身体质量指数(BMI)来衡量人体胖瘦成度以及是否健康,其计算公式是![]() .成人的BMI数值标准为:BMI
.成人的BMI数值标准为:BMI![]() 偏瘦;
偏瘦;![]() BMI
BMI![]() 为正常;
为正常;![]() BMI
BMI![]() 为偏胖;BMI
为偏胖;BMI![]() 为肥胖.某研究机构为了解某快递公司员工的身体质量指数,研究人员从公司员工体检数据中,抽取了8名员工(编号1-8)的身高
为肥胖.某研究机构为了解某快递公司员工的身体质量指数,研究人员从公司员工体检数据中,抽取了8名员工(编号1-8)的身高![]() (cm)和体重
(cm)和体重![]() (kg)数据,并计算得到他们的BMI(精确到0.1)如下表:
(kg)数据,并计算得到他们的BMI(精确到0.1)如下表:
编 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高(cm) | 163 | 164 | 165 | 168 | 170 | 172 | 176 | 182 |
体重(kg) | 54 | 60 | 77 | 72 | 68 | ● | 72 | 55 |
BMI(近似值) | 20.3 | 22.3 | 28.3 | 25.5 | 23.5 | 23.7 | 23.2 | 16.6 |
(1)现从这8名员工中选取3人进行复检,记抽取到BMI值为“正常”员工的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
(2)研究机构分析发现公司员工的身高![]() (cm)和体重
(cm)和体重![]() (kg)之间有较强的线性相关关系,在编号为6的体检数据丢失之前调查员甲已进行相关的数据分析,并计算得出该组数据的线性回归方程为
(kg)之间有较强的线性相关关系,在编号为6的体检数据丢失之前调查员甲已进行相关的数据分析,并计算得出该组数据的线性回归方程为![]() ,且根据回归方程预估一名身高为180cm的员工体重为71kg,计算得到的其它数据如下:
,且根据回归方程预估一名身高为180cm的员工体重为71kg,计算得到的其它数据如下:![]() ,
,![]() .
.
①求![]() 的值及表格中8名员工体重的平均值
的值及表格中8名员工体重的平均值![]() .
.
②在数据处理时,调查员乙发现编号为8的员工体重数据有误,应为63kg,身高数据无误,请你根据调查员乙更正的数据重新计算线性回归方程,并据此预估一名身高为180cm的员工的体重.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: 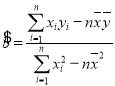 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域均为D的三个函数![]() ,
,![]() ,
,![]() 满足条件:对任意
满足条件:对任意![]() ,点
,点![]() 与点
与点![]() 都关于点
都关于点![]() 对称,则称
对称,则称![]() 是
是![]() 关于
关于![]() 的“对称函数”.已知函数
的“对称函数”.已知函数![]() ,
,![]() ,
,![]() 是
是![]() 关于
关于![]() 的“对称函数“,记
的“对称函数“,记![]() 的定义域为D,若对任意
的定义域为D,若对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,则实数a的取值范围是( )
成立,则实数a的取值范围是( )
A..![]() B..
B..![]() C..
C..![]() D..
D..![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
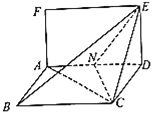
【题目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如图,其中
所在平面互相垂直,如图,其中![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ)试问在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?若存在,请证明
?若存在,请证明![]() 平面
平面![]() ,并求出
,并求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“二进制”来源于我国古代的《易经》,该书中有两类最基本的符号:“─”和“﹣﹣”,其中“─”在二进制中记作“1”,“﹣﹣”在二进制中记作“0”.如符号“”对应的二进制数011(2)化为十进制的计算如下:011(2)=0×22+1×21+1×20=3(10).若从两类符号中任取2个符号进行排列,则得到的二进制数所对应的十进制数大于2的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抑制房价过快上涨和过度炒作,各地政府响应中央号召,因地制宜出台了系列房价调控政策.某市拟定出台“房产限购的年龄政策”.为了解人们对“房产限购年龄政策”的态度,在2060岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如图所示:
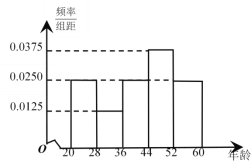
年龄 |
|
|
|
|
|
支持的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异?
44岁以下 | 44岁及44岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以44岁为分界点,从不支持“房产限购”的人中按分层抽样的方法抽取8人参加政策听证会,现从这8人中随机抽2人.记抽到44岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: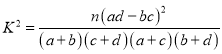 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com