
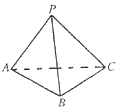
 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠BCA=90°,且BC=CA=2,PC=PA.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠BCA=90°,且BC=CA=2,PC=PA.分析 (1)由已知可得BC⊥AC,再由平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,且BC?平面ABC,得到BC⊥平面PAC,从而证得结论PA⊥BC;
(2)由(1)知PA⊥BC,只需PA⊥PC,就有PA⊥平面PBC,结合已知条件求出PC,进一步求出三棱锥P-ABC的体积.
解答 (1)证明:∵∠BCA=90°,∴BC⊥AC.
∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,且BC?平面ABC,
∴BC⊥平面PAC.
又PA?平面PAC.
∴PA⊥BC;
(2)解:由(1)知PA⊥BC,
故只需PA⊥PC,就有PA⊥平面PBC,
∵PC=PA,AC=2,
∴PC=$\sqrt{2}$.
此时,${V}_{P-ABC}=\frac{1}{3}•{S}_{△PBC}•AP$=$\frac{1}{3}×\frac{1}{2}×2×\sqrt{2}×\sqrt{2}=\frac{2}{3}$.
点评 本题考查直线与平面垂直,几何体的体积的求法,考查转化思想以及逻辑推理能力,是中档题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2+$\sqrt{5}$ | C. | 2+2$\sqrt{3}$ | D. | $\sqrt{7}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
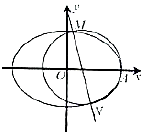 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,E的右焦点到直线y=x+1的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,E的右焦点到直线y=x+1的距离为$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\frac{\sqrt{2}}{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5p | B. | 10p | C. | 11p | D. | 12p |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0≤a<$\frac{1}{e}$ | B. | 0≤a<$\frac{1}{{e}^{2}}$ | C. | -$\frac{1}{e}$<a<$\frac{1}{{e}^{2}}$ | D. | 0≤a<$\frac{1}{e}$或a=-$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.30 | B. | 0.33 | C. | 0.35 | D. | 0.375 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com