
| A. | 1-$\frac{\sqrt{2}}{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
分析 由已知可得f(x+1)-f2(x+1)+f(x)-f2(x)=$\frac{1}{4}$,令g(x)=f(x)-f2(x),则g(0)+g(2017)=$\frac{1}{4}$,结合基本不等式和二次函数的图象和性质,可得答案.
解答 解:∵函数f(x)满足f(x+1)=$\frac{1}{2}$+$\sqrt{f(x)-{f}^{2}(x)}$,
∴f(x)>0且f2(x+1)=$\frac{1}{4}$+$\sqrt{f(x)-{f}^{2}(x)}$+f(x)-f2(x),
则f(x+1)-f2(x+1)=$\frac{1}{2}$+$\sqrt{f(x)-{f}^{2}(x)}$-[$\frac{1}{4}$+$\sqrt{f(x)-{f}^{2}(x)}$+f(x)-f2(x)]=$\frac{1}{4}$-[f(x)-f2(x)],
故f(x+1)-f2(x+1)+f(x)-f2(x)=$\frac{1}{4}$,
令g(x)=f(x)-f2(x),则g(x+1)+g(x)=$\frac{1}{4}$,
则g(0)=g(2)=…=g(2016); g(1)=g(3)=…=g(2017);
g(0)+g(2017)=$\frac{1}{4}$,
∴f(0)-f2(0)+f(2017)-f2(2017)=$\frac{1}{4}$,
f(0)+f(2017)=$\frac{1}{4}$+f2(0)+f2(2017)≥$\frac{1}{4}$+$\frac{[f(0)+f(2017)]^{2}}{2}$,
即2[f(0)+f(2017)]2-4[f(0)+f(2017)]+1≤0,
解得:f(0)+f(2017)∈[1-$\frac{\sqrt{2}}{2}$,1+$\frac{\sqrt{2}}{2}$],
故选:B
点评 本题考查的知识点是抽象函数的应用,函数求值,基本不等式的应用,难度中档.


科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面为梯形,且AB∥DC,DC=2AB,E和F分别是棱CD和PC的中点,PD⊥CD,PB=BC=BD=2$\sqrt{3}$,AB=2,二面角P-AB-D为$\frac{2π}{3}$.
如图,四棱锥P-ABCD的底面为梯形,且AB∥DC,DC=2AB,E和F分别是棱CD和PC的中点,PD⊥CD,PB=BC=BD=2$\sqrt{3}$,AB=2,二面角P-AB-D为$\frac{2π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.PO=$\sqrt{2}$,AB=2.求证:
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.PO=$\sqrt{2}$,AB=2.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,△PAC是边长为2的等边三角形,PB=$\sqrt{2}$,E为PA的中点.
在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,△PAC是边长为2的等边三角形,PB=$\sqrt{2}$,E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
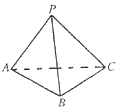 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠BCA=90°,且BC=CA=2,PC=PA.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠BCA=90°,且BC=CA=2,PC=PA.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\sqrt{2}})∪({\sqrt{2},+∞})$ | B. | $({-∞,-\frac{{\sqrt{2}}}{2}})$ | C. | $({-2,-\sqrt{2}})$ | D. | $({-∞,-\sqrt{2}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com