
分析 如图所示,以AP为z轴,AD为y轴,取BC的中点M,以AM为x轴,建立空间直角坐标系.设K(0,0,m),则$\overrightarrow{CK}$=$a\overrightarrow{CE}$+b$\overrightarrow{CF}$,可得K坐标.设平面PBD的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BD}=0}\\{\overrightarrow{n}•\overrightarrow{PD}=0}\end{array}\right.$,利用点K到平面PBD的距离d=$\frac{|\overrightarrow{n}•\overrightarrow{KP}|}{|\overrightarrow{n}|}$即可得出.
解答 解:如图所示,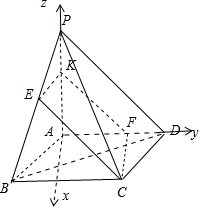
以AP为z轴,AD为y轴,取BC的中点M,以AM为x轴,建立空间直角坐标系.则A(0,0,0),P(0,0,3),D(0,3,0),F(0,2,0),B($\frac{3\sqrt{3}}{2}$,-$\frac{3}{2}$,0),C($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$,0),E($\frac{3\sqrt{3}}{4}$,-$\frac{3}{4}$,$\frac{3}{2}$),
设K(0,0,m),则$\overrightarrow{CK}$=$a\overrightarrow{CE}$+b$\overrightarrow{CF}$,
∴(0,0,m)=$(\frac{3\sqrt{3}}{2}-\frac{3\sqrt{3}a}{4}-\frac{3\sqrt{3}b}{2},\frac{3}{2}-\frac{9}{4}a+\frac{1}{2}b,\frac{3}{2}a)$,
∴$\frac{3\sqrt{3}}{2}-\frac{3\sqrt{3}}{4}$a-$\frac{3\sqrt{3}}{2}$b=0,$\frac{3}{2}-\frac{9}{4}a+\frac{1}{2}b$=0,$\frac{3}{2}$a=m,
解得m=$\frac{6}{5}$,a=$\frac{4}{5}$,b=$\frac{3}{5}$.
$\overrightarrow{BD}$=$(-\frac{3\sqrt{3}}{2},\frac{9}{2},0)$,$\overrightarrow{PD}$=(0,3,-3).
设平面PBD的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BD}=0}\\{\overrightarrow{n}•\overrightarrow{PD}=0}\end{array}\right.$,$\left\{\begin{array}{l}{-\frac{3\sqrt{3}}{2}x+\frac{9}{2}y=0}\\{3y-3z=0}\end{array}\right.$,
取$\overrightarrow{n}$=($\sqrt{3}$,1,1).
$\overrightarrow{KP}$=$(0,0,\frac{9}{5})$.
∴点K到平面PBD的距离d=$\frac{|\overrightarrow{n}•\overrightarrow{KP}|}{|\overrightarrow{n}|}$=$\frac{\frac{9}{5}}{\sqrt{5}}$=$\frac{9\sqrt{5}}{25}$.
故答案为:$\frac{9\sqrt{5}}{25}$.
点评 本题考查了空间位置关系、平面向量基本定理、法向量的应用、点到平面的距离公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:填空题
已知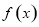 是定义在
是定义在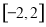 上的奇函数,当
上的奇函数,当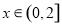 时,
时,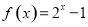 ,函数
,函数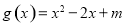 ,如果对于
,如果对于 ,使得
,使得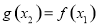 ,则实数
,则实数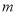 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\frac{\sqrt{2}}{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )
如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )| A. | 6$\sqrt{5}$-13 | B. | $\sqrt{5}$-2 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0≤a<$\frac{1}{e}$ | B. | 0≤a<$\frac{1}{{e}^{2}}$ | C. | -$\frac{1}{e}$<a<$\frac{1}{{e}^{2}}$ | D. | 0≤a<$\frac{1}{e}$或a=-$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AB⊥平面BCC1B1,$∠BC{C_1}=\frac{π}{3},AB=B{B_1}=2,BC=1,D$为CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AB⊥平面BCC1B1,$∠BC{C_1}=\frac{π}{3},AB=B{B_1}=2,BC=1,D$为CC1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com