
分析 (Ⅰ) 利用直接法点M的轨迹C的方程;利用特殊位置,即可求△ABM的周长的取值范围;
(Ⅱ) 直线MB与轨迹C的另一交点为M',$\frac{{S}_{△AMB}}{{S}_{△{AM}^{′}B}}$=|$\frac{{y}_{1}}{{y}_{2}}$|=t,利用韦达定理,即可求$\frac{{S}_{△AMB}}{{S}_{△{AM}^{′}B}}$的取值范围.
解答 解:(Ⅰ)设M(x,y),则由题意可得(x+4)2+y2=4(x+1)2+4y2,
化简可得x2+y2=4.
当M在(-2,0)时,|MA|+|MB|=3,M在(2,0)时,|MA|+|MB|=9,
∴△ABM的周长的取值范围是(6,12);
(Ⅱ) 设直线MB的方程为x=my-1,代入x2+y2=4,整理可得(m2+1)y2-2my-3=0,
设M(x1,y1),M′(x2,y2),则y1+y2=$\frac{2m}{{m}^{2}+1}$,y1y2=-$\frac{3}{{m}^{2}+1}$
$\frac{{S}_{△AMB}}{{S}_{△{AM}^{′}B}}$=|$\frac{{y}_{1}}{{y}_{2}}$|=t,则y1=-ty2,
联立3个方程可得$\frac{t}{(1-t)^{2}}$=$\frac{3}{4}$(1+$\frac{1}{{m}^{2}}$),
∴$\frac{t}{(1-t)^{2}}$>$\frac{3}{4}$,解得$\frac{1}{3}<t<3$,
∴$\frac{{S}_{△AMB}}{{S}_{△{AM}^{′}B}}$的取值范围是($\frac{1}{3}$,3).
点评 本题考查轨迹方程,考查直线与圆的位置关系的运用,考查学生的计算能力,属于中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面为梯形,且AB∥DC,DC=2AB,E和F分别是棱CD和PC的中点,PD⊥CD,PB=BC=BD=2$\sqrt{3}$,AB=2,二面角P-AB-D为$\frac{2π}{3}$.
如图,四棱锥P-ABCD的底面为梯形,且AB∥DC,DC=2AB,E和F分别是棱CD和PC的中点,PD⊥CD,PB=BC=BD=2$\sqrt{3}$,AB=2,二面角P-AB-D为$\frac{2π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4$\sqrt{2}$ | C. | 8 | D. | 8$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\sqrt{2}})∪({\sqrt{2},+∞})$ | B. | $({-∞,-\frac{{\sqrt{2}}}{2}})$ | C. | $({-2,-\sqrt{2}})$ | D. | $({-∞,-\sqrt{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
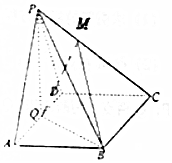 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com