
| A. | $({-∞,-\sqrt{2}})∪({\sqrt{2},+∞})$ | B. | $({-∞,-\frac{{\sqrt{2}}}{2}})$ | C. | $({-2,-\sqrt{2}})$ | D. | $({-∞,-\sqrt{2}})$ |
分析 根据题意,分析可得函数f(x)为奇函数且为增函数,进而可以将原问题转化为m<-$\frac{4}{t+\frac{2}{t}}$对任意实数t≥1恒成立,由基本不等式的性质分析可得-$\frac{4}{t+\frac{2}{t}}$有最小值-$\sqrt{2}$,进而分析可得m的取值范围.
解答 解:根据题意,函数f(x)=x3+3x,其定义域为R,关于原点对称,
有f(-x)=-(x3+3x)=-f(x),则f(x)为奇函数,
又由f′(x)=3x2+3>0,则f(x)为增函数,
若不等式f(2m+mt2)+f(4t)<0对任意实数t≥1恒成立,
则f(2m+mt2)<-f(4t),即2m+mt2<-4t对任意实数t≥1恒成立,
2m+mt2<-4t?m<-$\frac{4t}{{t}^{2}+2}$,即m<-$\frac{4}{t+\frac{2}{t}}$,
又由t≥1,则t+$\frac{2}{t}$≥2$\sqrt{2}$,则-$\frac{4}{t+\frac{2}{t}}$有最小值-$\sqrt{2}$,
若m<-$\frac{4}{t+\frac{2}{t}}$对任意实数t≥1恒成立,必有m<-$\sqrt{2}$;
即m的取值范围为(-∞,-$\sqrt{2}$);
故选:D.
点评 本题考查函数奇偶性与单调性的综合应用,关键是分析判断函数f(x)=x3+3x的奇偶性与单调性.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1-$\frac{\sqrt{2}}{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30.4<40.2<log0.40.5 | B. | ${3^{0.4}}<{log_{0.4}}0.5<{4^{0.2}}$ | ||
| C. | ${log_{0.4}}0.5<{3^{0.4}}<{4^{0.2}}$ | D. | ${log_{0.4}}0.5<{4^{0.2}}<{3^{0.4}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AB⊥平面BCC1B1,$∠BC{C_1}=\frac{π}{3},AB=B{B_1}=2,BC=1,D$为CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AB⊥平面BCC1B1,$∠BC{C_1}=\frac{π}{3},AB=B{B_1}=2,BC=1,D$为CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
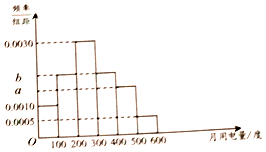 某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com