
| A. | 4 | B. | 4$\sqrt{2}$ | C. | 8 | D. | 8$\sqrt{2}$ |
分析 利用中点坐标公式及作差法,求得直线AB的斜率公式,求得直线直线AB的方程,代入抛物线方程,利用弦长公式及韦达定理,即可求得|AB|的值.
解答 解:设A(x1,y1),B(x2,y2),
则y12=4x1,y22=4x2,由中点坐标公式可知:y1+y2=4,
两式相减可得,(y1-y2)(y1+y2)=4(x1-x2),
则直线AB的斜率k,k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=1,
直线AB的方程为y-2=x-3即y=x-1,
联立方程可得$\left\{\begin{array}{l}{y=x-1}\\{{y}^{2}=4x}\end{array}\right.$,x2-6x+1=0,
丨AB丨=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$,
=$\sqrt{2}$•$\sqrt{{6}^{2}-4}$=8,
故选:C.
点评 本题考查直线与抛物线的位置关系,考查韦达定理,弦长公式,中点坐标公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )
如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )| A. | 6$\sqrt{5}$-13 | B. | $\sqrt{5}$-2 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 146石 | B. | 172石 | C. | 341石 | D. | 1358石 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 0 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30.4<40.2<log0.40.5 | B. | ${3^{0.4}}<{log_{0.4}}0.5<{4^{0.2}}$ | ||
| C. | ${log_{0.4}}0.5<{3^{0.4}}<{4^{0.2}}$ | D. | ${log_{0.4}}0.5<{4^{0.2}}<{3^{0.4}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
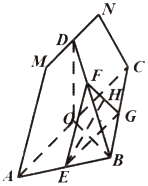 如图所示,四边形AMNC为等腰梯形,△ABC为直角三角形,平面AMNC与平面ABC垂直,AB=BC,AM=CN,点O、D、E分别是AC、MN、AB的中点.过点E作平行于平面AMNC的截面分别交BD、BC于点F、G,H是FG的中点.
如图所示,四边形AMNC为等腰梯形,△ABC为直角三角形,平面AMNC与平面ABC垂直,AB=BC,AM=CN,点O、D、E分别是AC、MN、AB的中点.过点E作平行于平面AMNC的截面分别交BD、BC于点F、G,H是FG的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com