
分析 求出AB垂直平分线的方程,利用圆O:x2+y2=9上存在点P,使得PA=PB,可得圆心到直线的距离d=$\frac{|{t}^{2}-12|}{\sqrt{16+4{t}^{2}}}$≤3,即可得出结论.
解答 解:由题意,kAB=$\frac{t}{-2}$,可得AB垂直平分线的方程为y-$\frac{t}{2}$=$\frac{2}{t}$(x-3),即4x-2ty+t2-12=0
∵圆O:x2+y2=9上存在点P,使得PA=PB,
∴圆心到直线的距离d=$\frac{|{t}^{2}-12|}{\sqrt{16+4{t}^{2}}}$≤3,
∴-2$\sqrt{15}$≤t≤2$\sqrt{15}$,
故答案为2$\sqrt{15}$.
点评 本题考查直线方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:解答题
已知函数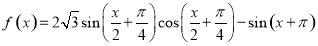 .
.
(1)求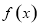 的最小正周期;
的最小正周期;
(2)若将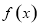 的图象向右平移
的图象向右平移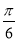 个单位,得到函数
个单位,得到函数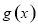 的图象,求函数
的图象,求函数 在区间
在区间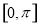 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:选择题
已知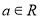 ,则“
,则“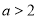 ”是“
”是“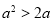 ”的( )
”的( )
A.充分非必条件 B.必要不充分条件
C.充要条件 D.既非充分也非必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,平面ABC⊥平面α,且平面ABC∩平面α=BC,AB=1,BC=$\sqrt{3}$,∠ABC=$\frac{5π}{6}$,平面α内一动点P满足∠PAB=$\frac{π}{6}$,则PC的最小值是$\frac{\sqrt{5}}{2}$.
如图,平面ABC⊥平面α,且平面ABC∩平面α=BC,AB=1,BC=$\sqrt{3}$,∠ABC=$\frac{5π}{6}$,平面α内一动点P满足∠PAB=$\frac{π}{6}$,则PC的最小值是$\frac{\sqrt{5}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面为梯形,且AB∥DC,DC=2AB,E和F分别是棱CD和PC的中点,PD⊥CD,PB=BC=BD=2$\sqrt{3}$,AB=2,二面角P-AB-D为$\frac{2π}{3}$.
如图,四棱锥P-ABCD的底面为梯形,且AB∥DC,DC=2AB,E和F分别是棱CD和PC的中点,PD⊥CD,PB=BC=BD=2$\sqrt{3}$,AB=2,二面角P-AB-D为$\frac{2π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
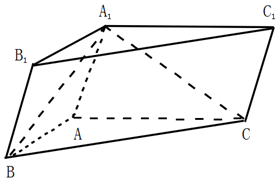 如图所示,在三棱柱ABC-A1B1C1中,AB=AC,四边形BCC1B1为矩形.
如图所示,在三棱柱ABC-A1B1C1中,AB=AC,四边形BCC1B1为矩形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,△PAC是边长为2的等边三角形,PB=$\sqrt{2}$,E为PA的中点.
在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,△PAC是边长为2的等边三角形,PB=$\sqrt{2}$,E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4$\sqrt{2}$ | C. | 8 | D. | 8$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com