
 在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,△PAC是边长为2的等边三角形,PB=$\sqrt{2}$,E为PA的中点.
在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,△PAC是边长为2的等边三角形,PB=$\sqrt{2}$,E为PA的中点.分析 (Ⅰ)证明BE⊥BC,利用BC∥AD,可得BE⊥AD,结合BE⊥PA,证明BE⊥平面PAD;
(Ⅱ)建立空间直角坐标系,求出平面PAC、PAD的一个法向量,即可求二面角C-PA-D的余弦值.
解答 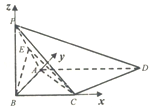 (Ⅰ)证明:∵△ABC与△ACD都是等腰直角三角形,∠ABC=∠ACD=90°,
(Ⅰ)证明:∵△ABC与△ACD都是等腰直角三角形,∠ABC=∠ACD=90°,
∴∠ACB=∠DAC=45°,$AC=\sqrt{2}BC$,∴BC∥AD,$AB=BC=\sqrt{2}$,
∵E为PA的中点,且$AB=PB=\sqrt{2}$,∴BE⊥PA,
在△PBC中,PC2=PB2+BC2,∴BC⊥PB.
又∵BC⊥AB,且PB∩AB=B,∴BC⊥平面PAB,
∵BE?平面PAB,∴BE⊥BC,
又∵BC∥AD,∴BE⊥AD,
又∵PA∩AD=A,∴BE⊥平面PAD;
(Ⅱ)解:由(Ⅰ)可以BC,AB,BP两两垂直,以B为原点,BC,AB,BP分别为x,y,z轴,建立空间直角坐标系,则$A({0,\sqrt{2},0})$,B(0,0,0),$C({\sqrt{2},0,0})$,$P({0,0,\sqrt{2}})$,则$\overrightarrow{AC}=({\sqrt{2},-\sqrt{2},0})$,$\overrightarrow{AP}=({0,-\sqrt{2},\sqrt{2}})$.
设平面PAC的一个法向量为$\overrightarrow m=({x,y,z})$,则$\left\{\begin{array}{l}\overrightarrow m•\overrightarrow{AC}=0\\ \overrightarrow m•\overrightarrow{AP}=0\end{array}\right.$∴$\left\{\begin{array}{l}x-y=0\\ y-z=0\end{array}\right.$∴取$\overrightarrow m=({1,1,1})$
又由(Ⅰ)知BE⊥平面PAD,故$\overrightarrow{BE}=({0,\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}})$为平面PAD的一个法向量,
∴$cos<\overrightarrow m$,$\overrightarrow{BE}>=\frac{{\sqrt{2}}}{{\sqrt{3}}}=\frac{{\sqrt{6}}}{3}$,
故二面角C-PA-D的余弦值$\frac{{\sqrt{6}}}{3}$.
点评 本题考查线面垂直的证明,考查面面角,考查向量方法的运用,正确求出平面的法向量是关键.


科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
已知点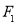 、
、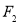 是双曲线
是双曲线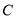 :
: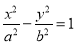 (
(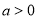 ,
,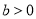 )的左、右焦点,
)的左、右焦点,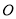 为坐标原点,点
为坐标原点,点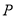 在双曲线
在双曲线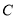 的右支上,且满足
的右支上,且满足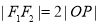 ,
,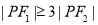 ,则双曲线
,则双曲线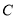 的离心率的取值范围为( )
的离心率的取值范围为( )
A.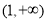 B.
B.
C.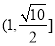 D.
D.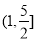
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\frac{\sqrt{2}}{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )
如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )| A. | 6$\sqrt{5}$-13 | B. | $\sqrt{5}$-2 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30.4<40.2<log0.40.5 | B. | ${3^{0.4}}<{log_{0.4}}0.5<{4^{0.2}}$ | ||
| C. | ${log_{0.4}}0.5<{3^{0.4}}<{4^{0.2}}$ | D. | ${log_{0.4}}0.5<{4^{0.2}}<{3^{0.4}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com