
在平面直角坐标系xOy中,已知对于任意实数k,直线( k+1)x+(k-
k+1)x+(k- )y-(3k+
)y-(3k+ )=0恒过定点F.设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为2+
)=0恒过定点F.设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为2+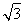 .
.
(1)求椭圆C的方程;
(2)设(m,n)是椭圆C上的任意一点,圆O:x2+y2=r2(r>0)与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
(1)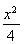 +y2=1.(2)直线l1与圆O相交,直线l2与圆O相离.
+y2=1.(2)直线l1与圆O相交,直线l2与圆O相离.
【解析】(1)由( k+1)x+(k-
k+1)x+(k-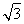 )y-(3k+
)y-(3k+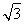 )=0整理
)=0整理
得(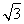 x+y-3)k+(x-
x+y-3)k+(x-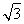 y-
y-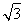 )=0,
)=0,
解方程组 得F(
得F(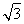 ,0).
,0).
设椭圆C的长轴长、短轴长、焦距分别为2a,2b,2c,则由题设知 于是a=2,b=1. 所以椭圆C的方程为
于是a=2,b=1. 所以椭圆C的方程为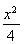 +y2=1.
+y2=1.
(2)因为圆O:x2+y2=r2(r>0)与椭圆C有4个相异公共点,所以b<r<a,即1<r<2.
因为点(m,n)是椭圆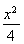 +y2=1上的点,所以
+y2=1上的点,所以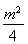 +n2=1,
+n2=1,
且-2≤m≤2.所以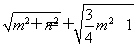 ∈[1,2].
∈[1,2].
于是圆心O到直线l1的距离d1=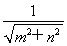 ≤1<r,
≤1<r,
圆心O到直线l2的距离d2=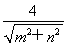 ≥2>r.
≥2>r.
故直线l1与圆O相交,直线l2与圆O相离


科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用20练习卷(解析版) 题型:解答题
如图,在四棱锥O ?ABCD中,底面ABCD为菱形,OA⊥平面ABCD,E为OA的中点,F为BC的中点,求证:(1)平面BDO⊥平面ACO;(2)EF∥平面OCD.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(解析版) 题型:解答题
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.

(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C?PB?A的余弦值..
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用13练习卷(解析版) 题型:解答题
如图,点P(0,-1)是椭圆C1: =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.

(1)求椭圆C1的方程;
(2)求△ABD面积取最大值时直线l1的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用13练习卷(解析版) 题型:填空题
已知椭圆 =1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为________.
=1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(解析版) 题型:填空题
已知椭圆E: =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为________.
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(解析版) 题型:填空题
直线 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为________.
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用10练习卷(解析版) 题型:填空题
在等差数列{an}中,a1=142,d=-2,从第一项起,每隔两项取出一项,构成新的数列{bn},则此数列的前n项和Sn取得最大值时n的值是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练2练习卷(解析版) 题型:选择题
如图,设点A是单位圆上的一定点,动点P从A出发在圆上按逆时针方向旋转一周,点P所转过的弧AP的长为l,弦AP的长度为d,则函数d=f(l)的图象大致是( )
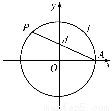
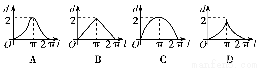
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com