
【题目】已知函数![]() 为偶函数,且在
为偶函数,且在![]() 上单调递减,则
上单调递减,则![]() 的解集为
的解集为![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线C1的参数方程为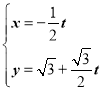 (t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2(1+sin2θ)=2,点M的极坐标为(
(t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2(1+sin2θ)=2,点M的极坐标为(![]() ,
,![]() ).
).
(1)求点M的直角坐标和C2的直角坐标方程;
(2)已知直线C1与曲线C2相交于A,B两点,设线段AB的中点为N,求|MN|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个正方形花圃被分成5份.

(1)若给这5个部分种植花,要求相邻两部分种植不同颜色的花,己知现有红、黄、蓝、绿4种颜色不同的花,求有多少种不同的种植方法?
(2)若向这5个部分放入7个不同的盆栽,要求每个部分都有盆栽,问有多少种不同的放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第一次大考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于![]() 分为优秀,
分为优秀,![]() 分以下为非优秀,统计成绩后,得到如下
分以下为非优秀,统计成绩后,得到如下![]() 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部![]() 人中随机抽取
人中随机抽取![]() 人为优秀的概率为
人为优秀的概率为![]() .
.
(I)请完成![]() 列联表:
列联表:
优秀 | 非优秀 | 合计 | |
甲班 |
| ||
乙班 |
| ||
合计 |
|
(Ⅱ)根据列联表的数据能否在犯错误的概率不超过![]() 的前提下认为成绩与班级有关系?
的前提下认为成绩与班级有关系?
参考公式和临界值表:
 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业2018年招聘员工,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
岗位 | 男性 应聘人数 | 男性 录用人数 | 男性 录用比例 | 女性 应聘人数 | 女性 录用人数 | 女性 录用比例 |
| 269 | 167 |
| 40 | 24 |
|
| 40 | 12 |
| 202 | 62 |
|
| 177 | 57 |
| 184 | 59 |
|
| 44 | 26 |
| 38 | 22 |
|
| 3 | 2 |
| 3 | 2 |
|
总计 | 533 | 264 |
| 467 | 169 |
|
(1)从表中所有应聘人员中随机选择1人,试估计此人被录用的概率;
(2)从应聘![]() 岗位的6人中随机选择2人.记
岗位的6人中随机选择2人.记![]() 为这2人中被录用的人数,求
为这2人中被录用的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于
各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于![]() ),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)
),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x﹣3≤0},B={x|x2﹣2mx+m2﹣4≤0,x∈R,m∈R}.
(1)若A∪B=A,求实数m的取值;
(2)若A∩B={x|0≤x≤3},求实数m的值;
(3)若A![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数f(x)和奇函数g(x)满足![]() .
.
(1)求函数f(x)和g(x)的表达式;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若方程![]() 在
在![]() 上恰有一个实根,求实数m的取值范围.
上恰有一个实根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下给出了4个命题:
(1)两个长度相等的向量一定相等;
(2)相等的向量起点必相同;
(3)若![]() ,且
,且![]() ,则
,则![]() ;
;
(4)若向量![]() 的模小于
的模小于![]() 的模,则
的模,则![]() .
.
其中正确命题的个数共有( )
A.3 个B.2 个C.1 个D.0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com