分析:(1)根据已知中D是BC的中点,我们可得AD⊥面CC1B1B,进而AD⊥B1F,FD⊥B1F,结合线面垂直的判定定理即可得到B1F⊥平面ADF;
(2)延长FD、B1B交于G,则AG为所求二面角的棱,过B1作B1H⊥AG,且B1H与AG交于H,可得∠B1HF为所求二面角的平面角,解三角形B1HF即可得到平面ADF与平面AA1B1B所成角的正弦值.
解答:证明:(1)因为AB=AC,D是BC的中点,所以AD⊥BC.
又侧面CC
1B
1B⊥平面ABC,所以AD⊥面CC
1B
1B
又B
1F?面CC
1B
1B,所以AD⊥B
1F
在Rt△B
1C
1F中,tan∠C
1B
1F=
,在Rt△DCF中 tan∠CFD=
,
所以∠C
1B
1F=∠CFD,∠C
1FB
1+∠CFD=
-∠C
1B
1F+∠CFD=
,∠B
1FD=π-(∠C
1FB
1+∠CFD)=
即FD⊥B
1F,所以B
1F⊥平面ADF;.…(6分)
解:(2)延长FD、B
1B交于G,则AG为所求二面角的棱.由Rt△FCD≌Rt△GBD得:CF=GB=2a.
过B
1作B
1H⊥AG,且B
1H与AG交于H,又 B
1F⊥平面ADF,FH⊥AG,
∠B
1HF为所求二面角的平面角.
由Rt△ABG和Rt△B
1HD相似得:B
1H=
.又B
1F=
=
a,所以 sin∠B
1HF=
.
即所求二面角的正弦值是
.…(12分)
点评:本题考查的知识点是直线与平面垂直的判定,二面角的平面角及求法,其中(1)的关键是证明出AD⊥B1F,FD⊥B1F,(2)的关键是求出∠B1HF为所求二面角的平面角.

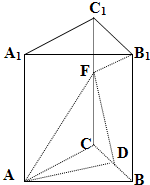 (2010•舟山模拟)在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是CC1上一点,且CF=2a.
(2010•舟山模拟)在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是CC1上一点,且CF=2a.
