
(1)若过A点的抛物线的切线与y轴相交于C点,求证:|AF|=|CF|;
(2)若![]() ·
·![]() +p2=0(A、B异于原点),直线OB与m相交于点P,试求P点的轨迹方程;
+p2=0(A、B异于原点),直线OB与m相交于点P,试求P点的轨迹方程;
(3)若AB为焦点弦,分别过A、B点的抛物线的两条切线相交于点T,求证:AT⊥BT,且T点在l上.
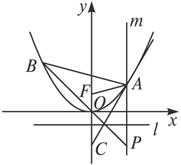
(1)证明:如图,设A(x1,y1),
∵y′=![]() ,
,
∴kAC=![]() .
.
于是AC的方程为y-y1=![]() (x-x1),即y=
(x-x1),即y=![]() x-y1.
x-y1.
令x=0,得y=-y1,即C(0,-y1).
由定义,|AF|=y1+![]() .
.
又|CF|=![]() -(-y1)=y1+
-(-y1)=y1+![]() ,
,
故|AF|=|CF|.
(2)解:设A(x1,y1),B(x2,y2),P(x,y),
![]() ·
·![]() +p2=0
+p2=0![]() x1x2+y1y2+p2=0
x1x2+y1y2+p2=0![]() x1x2+
x1x2+![]() +p2=0
+p2=0![]() (
(![]() +p)2=0.
+p)2=0.
∴x1x2=-2p2.
直线OB的方程为y=![]() x=
x=![]() x, ①
x, ①
直线m的方程为x=x1, ②
①×②得xy=![]() x
x![]() xy+px=0,
xy+px=0,
∵x≠0,∴y=-p.
故P点的轨迹方程为y=-p.
(3)证明:设A(x1,y1)、B(x2,y2)、T(x0,y0),则kAT=![]() ,kBT=
,kBT=![]() .
.
由于AB是焦点弦,可设AB的方程为y=kx+![]() ,代入x2=2py,得x2-2pkx-p2=0.∴x1x2=-p2.
,代入x2=2py,得x2-2pkx-p2=0.∴x1x2=-p2.
于是kAT·kBT=![]() =-1,故AT⊥BT.
=-1,故AT⊥BT.
由(1)知,AT的方程为y=![]() x-y1,
x-y1,
∴y0=![]() x0-y1,即x0x1-py1=py0.
x0-y1,即x0x1-py1=py0.
同理,x0x2-py2=py0,
∴AB的方程为x0x-py=py0.
又∵AB过焦点,∴-![]() =py0,即y0=-
=py0,即y0=-![]() .
.
故T点在准线l上.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
| a2 |
| 16 |
| a2 |
| 16 |
| a2 |
| 4 |
| a2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| sin2θ |
| a |
| sin2θ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a2 |
| 8sinθ |
| a2 |
| 8sinθ |
查看答案和解析>>
科目:高中数学 来源:江西省浮梁一中2007届高三数学重组卷二(人教版) 题型:044
已知AB是抛物线x2=2py(p>0)的任一弦,F为抛物线的焦点,l为准线.m为过A点且以![]() 为方向向量的直线.
为方向向量的直线.
(1)若过![]() 点的抛物线的切线与y轴相交于C点,求证:|AF|=|CF|;
点的抛物线的切线与y轴相交于C点,求证:|AF|=|CF|;
(2)若![]() (A、B异于原点),直线OB与m相交于点M,试求点M的轨迹方程;
(A、B异于原点),直线OB与m相交于点M,试求点M的轨迹方程;
(3)若AB为焦点弦,分别过A、B点的抛物线的两条切线相交于点T,求证:AT⊥BT,且T点在l上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com